Có bao nhiêu số nguyên m ∈ - 10 ; 10 để hàm số y = m 2 x 4 - 2 4 m - 1 x 2 + 1 đồng biến trên khoảng 1 ; + ∞
A. 15
B. 7
C. 16
D. 6
Những câu hỏi liên quan
Có bao nhiêu số nguyên m<10 để phương trình m + m + e x = e x có nghiệm thực.
A. 9.
B. 8.
C. 10.
D. 7.
Có bao nhiêu số nguyên m để tập nghiệm của bất phương trình
3
x
+
2
-
3
3
x
-
m
0
chứa đúng 10 số nguyên ? A. B. C. D.
Đọc tiếp
Có bao nhiêu số nguyên m để tập nghiệm của bất phương trình 3 x + 2 - 3 3 x - m < 0 chứa đúng 10 số nguyên ?
A.
B.
C.
D.
Có bao nhiêu số nguyên m để tập nghiệm của bất phương trình
3
x
+
2
-
3
3
x
-
m
0
chứa đúng 10 số nguyên A.
3
10
-...
Đọc tiếp
Có bao nhiêu số nguyên m để tập nghiệm của bất phương trình 3 x + 2 - 3 3 x - m < 0 chứa đúng 10 số nguyên
A. 3 10 - 3 9
B. 3 9 - 3 8 - 1
C. 3 10 - 3 9 - 1
D. 3 9 - 3 8
Có 
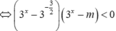
+) Nếu
m
≤
0
bất phương trình tương đương với 
chứa vô số các số nguyên (loại);
+) Nếu 0 < m < 3 - 3 2 không có số nguyên m nào cả (loại).
+) Nếu
m
>
3
-
3
2
bất phương trình tương đương với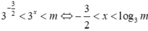 
Tập nghiệm là 
Vì S chứa đúng 10 số nguyên do đó 
⇒
m
∈
3
8
+
1
,
.
.
.
,
3
9
Có tất cả
3
9
-
3
8
số nguyên thoả mãn.
Chọn đáp án D.
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên m < 10 để hàm số y = | x 3 - m x + 1 | có 5 điểm cực trị.
A. 9.
B. 7.
C. 11.
D. 8.
Có bao nhiêu số nguyên m < 10 để hàm số y = x 3 - m x + 1 có 5 điểm cực trị.
A. 9.
B. 7.
C. 11.
D. 8.
Có bao nhiêu giá trị nguyên của tham số m (m < 10) để phương trình 2 x - 1 = log 4 x + 2 m + m có nghiệm ?
A.9
B.10
C.5
D.4
Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình m + m + e x = e x có nghiệm thực?
A. 9
B. 10
C. 11
D. Vô số
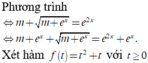và đi đến kết quả
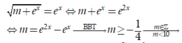có 10 giá trị thỏa mãn. Chọn B.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10; 10] để phương trình m x 2 - m x + 1 = 0 có nghiệm.
A. 17
B. 18
C. 20
D. 21
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên m<10 để hàm số y = x 3 - 3 x 2 + m x đồng biến trên R?
A. 7.
B. 8.
C. 6.
D. 5
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
x
+
2
x
+
m
đồng biến trên khoảng
-
∞
;
-
10
? A. 7. B. Vô số. C. 9. D. 8.
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x + 2 x + m đồng biến trên khoảng - ∞ ; - 10 ?
A. 7.
B. Vô số.
C. 9.
D. 8.
Vậy có 8 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án D
Đúng 0
Bình luận (0)