Trong các số phức z thỏa mãn z = z - 2 + 4 i , số phức có môđun nhỏ nhất là.
A. z =5
B. z = 5 2 i
C. z = 1 +2i
D. z = 3+i
Những câu hỏi liên quan
Trong các số phức z thỏa mãn |z + 4 - 3i| + |z -8 - 5i| = 2 38 . Tìm giá trị nhỏ nhất của |z – 2 – 4i| ?
A. 1/2
B. 5/2
C. 2
D. 1
Chọn D.
Gọi M( x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Khi đó 
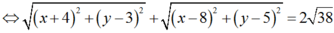
Áp dụng bất đẳng thức Bunhiakovsky ta có:
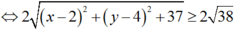
Vậy Min|z – 2 – 4i| = 1
Đúng 0
Bình luận (0)
Trong các số phức z thỏa mãn điều kiện z - 2 + 4 i = z - 2 i . Số phức z có môđun nhỏ nhất là?
A. z = -2 + 2i.
B. z = 2 - 2i.
C. z = 2 + 2i.
D. z = 2 - 2i.
Chọn C.
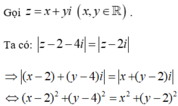
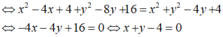
Do đó tập hợp các điểm biểu diễn số phức z là đường thẳng có phương trình x + y – 4 = 0
Mặt khác
Đúng 0
Bình luận (0)
Trong các số phức z thỏa mãn
|
z
-
1
-
2
i
|
+
|
z
+
2
-
3
i
|
10
. Modun nhỏ nhất của số phức z là A.
9
10
10
B.
3
10
10
C. ...
Đọc tiếp
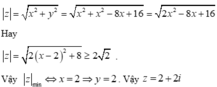
Trong các số phức z thỏa mãn | z - 1 - 2 i | + | z + 2 - 3 i | = 10 . Modun nhỏ nhất của số phức z là
A. 9 10 10
B. 3 10 10
C. 7 10 10
D. 10 5
Trong các số phức z thỏa mãn điều kiện |z-2-4i|=|z-2i|. Số phức z có môđun nhỏ nhất là?
A. z = -2+2i
B. z = 2-2i
C. z = 2+2i
D. z = -2-2i
Trong các số phức z thỏa mãn điều kiện z - 2 - 4 i = z - 2 i .Tìm số phức z có môđun nhỏ nhất
A. z = -2 +2i
B. z = -1 +i
C. z = 3+ 2i
D. z = 2 +2i
Trong các số phức z thỏa mãn
z
-
1
-
2
i
+
z
-
2
+
3
i
10
Modun nhỏ nhất của số phức z là
Đọc tiếp
Trong các số phức z thỏa mãn z - 1 - 2 i + z - 2 + 3 i = 10 Modun nhỏ nhất của số phức z là
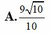
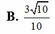
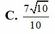
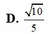
Trong các số phức z thỏa mãn điều kiện z - 2 - 4 i = z - 2 i .Tìm số phức z có môđun nhỏ nhất
A. z = -2 +2i
B. z = -1 +i
C. z = 3 +2i
D. z = 2 +2i
Trong các số phức z thỏa mãn
z
+
4
−
3
i
+
z
−
8
−
5
i
2
38
. Tìm giá trị nhỏ nhất của
z
−
2
−
4...
Đọc tiếp
Trong các số phức z thỏa mãn z + 4 − 3 i + z − 8 − 5 i = 2 38 . Tìm giá trị nhỏ nhất của z − 2 − 4 i
A. 1 2
B. 5 2
C. 2
D. 1
Trong các số phức z thỏa mãn
z
+
4
-
3
i
+
z
-
8
-
5
i
2
38
. Tìm giá trị nhỏ nhất của
z
-
2
-
4
i
. A.
1
2...
Đọc tiếp
Trong các số phức z thỏa mãn z + 4 - 3 i + z - 8 - 5 i = 2 38 . Tìm giá trị nhỏ nhất của z - 2 - 4 i .
A. 1 2
B. 5 2
C. 2
D. 1
Đáp án D.
Đặt z = x + y i , ( x , y ∈ ℝ ) .
Từ giả thiết ta có: x + 4 + y - 3 i + ( x - 8 ) + ( y - 5 ) i = 2 38
⇔ x + 4 2 + y - 3 2 + x - 8 2 + y - 5 2 = 2 38 .
Áp dụng bất đẳng thức Bunyakovsky, ta có:
x + 4 2 + y - 3 2 + x + 8 2 + y - 5 2 ≤ ( 1 2 + 1 2 ) x + 4 2 + ( y - 3 ) 2 + ( x - 8 ) 2 + ( y - 5 ) 2 = 2 x 2 - 4 + y 2 - 8 y + 57 ⇔ 38 ≤ x - 2 2 + y - 4 2 + 37 ⇔ x - 2 2 + y - 4 2 ≥ 1
Lại có z - 2 - 4 i = x - 2 + ( y + 4 ) i = x - 2 2 + ( y - 4 ) 2 ≥ 1 = 1 .
Đúng 0
Bình luận (0)