Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x) = 1 2 x - x + 1 trên đoạn [0;3]. Tính tổng S = 2m + 3M
A. S = - 7 2
B. S = - 3 2
C. S = -3
D. S = 4
Cho hàm số f ( x ) = x 3 - 3 x . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=|f(sinx+1)+2|. Giá trị biểu thức M + m bằng
A. 4.
B. 6.
C. 2.
D. 8.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = 2 x 3 + 3 x 2 - 1 trên đoạn - 2 ; - 1 2 . Tính P=M-m.
A. P=-5
B. P=1
C. P=5
D. P=4
f ( x ) = 2 x 3 + 3 x 2 - 1 ⇒ f ' ( x ) = 6 x 2 + 6 x ; f ' ( x ) = 0 ⇔ [ x = 0 ( k t m ) x = - 1 ( t m )
Hàm số f(x) liên tục trên - 2 ; - 1 2 ,
có f ( - 0 ) = - 5 ; f ( - 1 ) = 0 ; f - 1 2 = - 1 2
⇒ m = m i n - 2 ; - 1 2 f ( x ) = - 5 ; M = m a x - 2 ; - 1 2 f ( x ) = 0 ⇒ P = M - m = 5
Chọn đáp án C.
Cho hàm số y=f(x), x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn - 2 ; 3 . Giá trị của M+n là
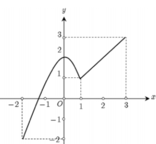
A. 6
B. 1
C. 5
D. 3
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = 2x - 4 6 - x trên [-3;6]. Tổng M + m có giá trị là
A. -12
B. -6
C. 18
D. -4
Chọn B
Hàm số f(x) xác định và liên tục trên [-3;6].
![]()
Ta có: ![]()
Khi đó: ![]()
Vậy: M + m = 12 + (-18) = -6
Cho hàm số y=f(x), x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn - 2 ; 3 . Giá trị của S=M+m là:
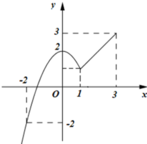
A. 6
B. 3
C. 5
D. 1
Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f(x) = x 2 - 3 x + 6 x - 1 trên đoạn [2;4] lần lượt là M, m. Tính S= M + m
A. S = 7
B. S= 3
C. S= 6
D. S= 4
Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = x 2 - 3 x + 6 x - 1 trên đoạn [2;4] lần lượt là M, m. Tính S = M + m
![]()
![]()
![]()
![]()
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = 2 x - 4 - 6 - x trên [-3;6]. Tổng M+m có giá trị là
A. -12
B. -6
C. 18
D. -4
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x) = 2x + 5 - x 2 . Giá trị của m 2 + M bằng
A. 5
B. 25
C. 5 + 2 5
D. 45
Chọn B
Hàm số xác định và liên tục trên đoạn [- 5 ; 5 ]
Ta có 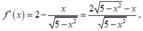
![]()
![]()
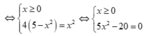
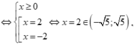
Ta có: ![]()
![]()
Suy ra ![]()
![]()
![]()