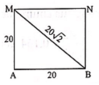
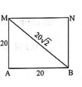
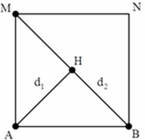
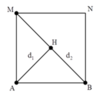
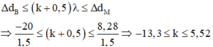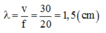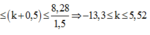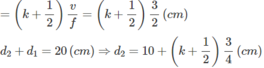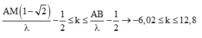Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 40 cm, dao động theo phương thẳng đứng với phương trình x A = x B = 3 cos 20 πt mm (t đo bằng s). Biết tốc độ truyền sóng trên mặt chất lỏng là 30 cm/s. Coi biên độ sóng mỗi nguồn truyền đi trên mặt chất lỏng là không đổi. Trên đường nối A,B số điểm dao động với biên độ 3 2 mm là
A. 54
B. 27
C. 26
D. 53