Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số y = x 4 - 38 x 2 + 120 x + 4 m trên đoạn 0 ; 2 đạt giá trị nhỏ nhất.
A. 26
B. 13
C. 14
D. 27
Cho hàm số y = m sin x + 1 cos x + 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5; 5] để giá trị nhỏ nhất của y nhỏ hơn -1
A. 6
B. 3
C. 4
D. 5
Có bao nhiêu giá trị nguyên dương của tham số m để giá trị nhỏ nhất của hàm số y = x + m 2 x - 1 trên đoạn [2;3] bằng 14.
A. 2
B. 1
C. 0
D. 4
Chọn B
Tập xác định D = ℝ \{1}
Ta có 
Do đó hàm số nghịch biến trên đoạn [2;3]
Suy ra ![]()
Vậy có 1 giá trị nguyên dương của m.
Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số y = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] đạt giá trị nhỏ nhất
A. 26
B. 13
C. 14
D. 27
Xét u = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có
![]()
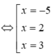
Vậy
Khi đó
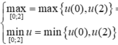
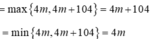
![]()
⇔ - 26 ≤ m ≤ 0
Có 27 số nguyên thoả mãn.
Chọn đáp án D.
Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số y = | x 4 - 38 x 2 + 120 x + 4 m | trên đoạn [0;2] đạt giá trị nhỏ nhất.
A. 26
B. 13
C. 14
D. 27
Chọn D
Xét ![]() trên đoạn [0;2], ta có:
trên đoạn [0;2], ta có:
Vậy 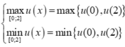
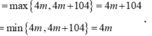
Cách 1:
Nếu 4m > 0 thì ![]()
Nếu 4m + 104 < 0
⇔
m < -126 thì ![]()
Nếu ![]() thì
thì ![]() Vậy có 27 số nguyên thỏa mãn.
Vậy có 27 số nguyên thỏa mãn.
Cách 2:
Khi đó ![]()
![]()
Có 27 số nguyên thoả mãn.
Cho hàm số y = m . sin x + 1 cos x + 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng - 10 ; 10 để giá trị nhỏ nhất của y nhỏ hơn -1.
A. 14
B. 13
C. 12
D. 15
Cho hàm số y = m sin x + 1 cos x + 1 . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5;5] để giá trị nhỏ nhất của y nhỏ hơn -1
A. 6
B. 5
C. 4
D. 3
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y = m sin x + 1 cos x + 2 nhỏ hơn 2?
A. 5
B. 3
C. 4
D. 6
Đáp án A
Giả sử giá trị lớn nhất của hàm số là M. Khi đó
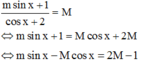
có nghiệm
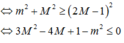
xét ![]()
Có ![]()
Suy ra ![]() có 2 nghiệm phân biệt
có 2 nghiệm phân biệt
![]()
Ta có
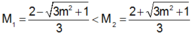
suy ra 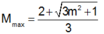
Yêu cầu bài toán
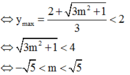
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y = m sin x + 1 cos x + 2 nhỏ hơn 2?
A. 5
B. 3
C. 4
D. 6
Cho hàm số y = m sin x + 1 cos x + 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5; 5] để giá trị nhỏ nhất của y nhỏ hơn -1.
![]()
![]()
![]()
![]()