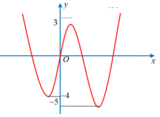
Hình vẽ bên là đồ thị của hàm số y = a x 4 + b x 2 + c . Giá trị của biểu thức M = a 2 + b 2 + c 2 có thể nhận giá trị nào trong các giá trị sau
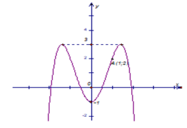
A. M = 18
B. M = 6
C. M = 20
D. M = 24
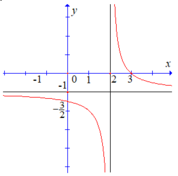
Cho hàm số y = x - a b x + c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c
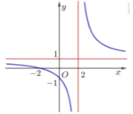
A. - 2
B. -3
C. - 4
D. -5
Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số có TCĐ và TCN là
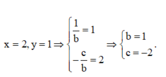
Đồ thị hàm số đi qua điểm có tọa độ ( -2; 0) nên a= -2
Suy ra A= a+ b+ c= -2+ 1+ ( -2) = -3
Chọn B.
Cho hàm số y = x − a b x + c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức P=a+b+c
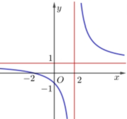
A. P = - 3
B. P = 1
C. P = 5
D. P = 2
Cho hàm số y=f(x) là hàm đa thức hệ số thực. Hình vẽ bên là đồ thị của hai hàm số y=f(x) và y=f'(x) . Phương trình f(x)= m e x có hai nghiệm thực phân biệt thuộc đoạn [0;2] khi và chỉ khi m thuộc nửa khoảng [a;b). Giá trị của a+b gần nhất với giá trị nào dưới đây ?
A. 0,27.
B. −0,54.
C. −0,27.
D. 0,54.
Cho hàm số y=f(x) là hàm đa thức với hệ số thực. Hình vẽ bên dưới là một phần đồ thị của hai hàm số: y=f(x) và y=f'(x)
Tập các giá trị của tham số m để phương trình f ( x ) = m e x có hai nghiệm phân biệt trên [0;2] là nửa khoảng [a;b). Tổng a+b gần nhất với giá trị nào sau đây?
A. -0.81
B. -0.54
C. -0.27
D. 0.27
Cho hàm số y = ax + b x + c có đồ thị như hình vẽ bên dưới.
Giá trị của biểu thức a+2b+c bằng
A. -2
B. 0
C. 3
D. -1
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
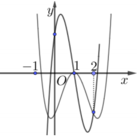
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f ( x ) + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tính tổng T = a + b.
A. T = 2
B. T = 1
C. T = -1
D. T = -2
Đáp án A
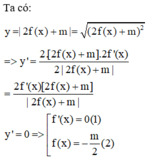
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy
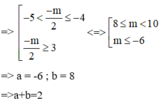
Cho hàm số y=f(x) có đồ thị (C) như hình vẽ bên và có đạo hàm f'(x) liên tục trên khoảng (-∞;+∞).Đường thẳng ở hình vẽ bên là tiếp tuyến của (C) tại điểm có hoành độ x=0. Gọi m là giá trị nhỏ nhất của hàm số y=f'(x). Mệnh đề nào dưới đây đúng ?
A. m < -2
B. -2 < m < 0.
C. 0 < m < 2
D. m > 2
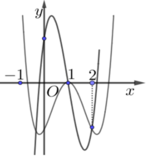
Cho đồ thị hàm số y = f(x) như hình vẽ bên. Giá trị m để đường thẳng y = 2m cắt đồ thị hàm số y = f x tại 4 điểm phân biệt là
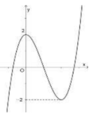
A. − 2 < m < 2
B. − 1 ≤ m ≤ 1
C. − 1 < m < 1
D. m = 1
Đáp án C.
Đồ thị hàm số y = f x C 1 được suy ra từ đồ thị của hàm số y = f x C như sau:
+ Hàm số y = f x là hàm chẵn có đồ thị đối xứng qua trục tung
+ Hàm số y = f x = f x , x ≥ 0 − f x , x < 0
+ Đồ thị hàm số y = f x gồm hai phần
Phần 1: Là đồ thị (C) ở bên phải trục Oy
Phần 2: Đối xứng của phần 1 qua Oy
+ Vẽ đồ thị C 1 như hình vẽ
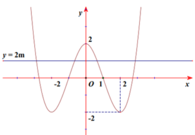
Để đường thẳng y = 2m cắt C 1 tại 4 điểm phân biệt khi − 2 < 2 m < 2 ⇔ − 1 < m < 1