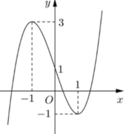
Cho hàm số y = f x liên tục trên R và có đồ thị như hình vẽ bên. Gọi S là tập hợp tất cả các số nguyên m để phương trình f sin x = 3 sin x + m có nghiệm thuộc khoảng 0 ; π .Tổng các phần tử của S bằng
A. -5.
B. -8.
C. -6.
D. -10.
Câu 23: Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị như hình vẽ bên. Hàm số y = f(3 - 2x) tăng trên khoảng nào:

Hình 3: Đồ thị y=f(x)

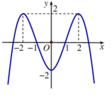
Cho hàm số y=f(x) liên tục trên R và có đồ thị là đường cong như hình vẽ bên. Tìm điểm cực tiểu của đồ thị hàm số y=f(x).
A. y=-2
B. x=0
C. M(0;-2)
D. N(2;2)
Đáp án C
Nhìn vào đồ thị thì điểm cực tiểu là điểm M(0;-2)
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ.
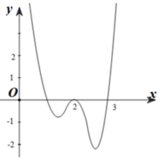
Hỏi hàm số y=f(f(x)) có bao nhiêu điểm cực trị ?
A. 6
B. 8
C. 7
D. 9
Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y = f'(x) như hình vẽ. Hàm số y = f ( 2 x 2 + x ) có bao nhiêu cực trị?
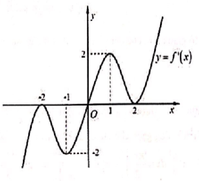
A. 4.
B. 5.
C. 3.
D. 1.
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f(x) như hình vẽ
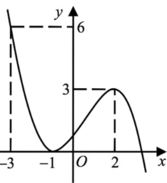
Tích phân ∫ 0 1 f ' 5 x - 3 d x bằng
A. 0,6
B. 1,8
C. 45
D. 15
Đổi biến ![]()
![]()
Do đó
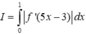
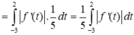

Trên đoạn [-3;-1] đồ thị f(t) đi xuống nên ![]() trên đoạn [-1;2] đồ thị f(t) đi lên nên
trên đoạn [-1;2] đồ thị f(t) đi lên nên ![]()
Vì vậy
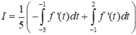
![]()
![]()
Chọn đáp án B.
Cho hàm số y=f(x) có đạo hàm liên tục trên R và đồ thị hàm số y=f’(x) như hình vẽ. Khẳng định sau đây là sai?
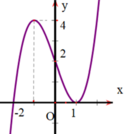
A. Hàm số y = f(x) đồng biến trên khoảng (1;+∞)
B. Hàm số y = f(x) đồng biến trên khoảng (-2;-1)
C. Hàm số y = f(x) nghịch biến trên khoảng (-1;1)
D. Hàm số y = f(x) nghịch biến trên khoảng (-∞;-2)
Cho hàm số y = f(x) có đạo hàm liên tục trên R và hàm số y= f’(x) có đồ thị như hình vẽ bên.
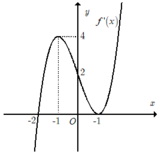
Mệnh đề nào sau đây đúng?
A. Hàm số y= f( x) đạt cực đại tại điểm x= -1
B. Hàm số y= f( x) đạt cực tiểu tại điểm x= 1
C. Hàm số y= f(x) đạt cực tiểu tại điểm x= -2
D. Hàm số y= f(x) đạt cực đại tại điểm x= -2.
Chọn C
+ ta có: f’( x) = 0 khi x= -1 hoặc x= -2.
+ Giá trị của hàm số y= f’(x) không đổi dấu khi đi qua x= - 1 nên x= -1 không là điểm cực trị của hàm số.
+ Giá trị của hàm số y= f’(x) đổi dấu từ âm sang dương khi qua x= -2
=> Hàm số y= f(x) đạt cực tiểu tại điểm x= -2.
Cho hàm số y= f(x) liên tục trên R. Hàm số y= f’(x) có đồ thị như hình vẽ. Hàm số ![]() có bao nhiêu cực trị?
có bao nhiêu cực trị?
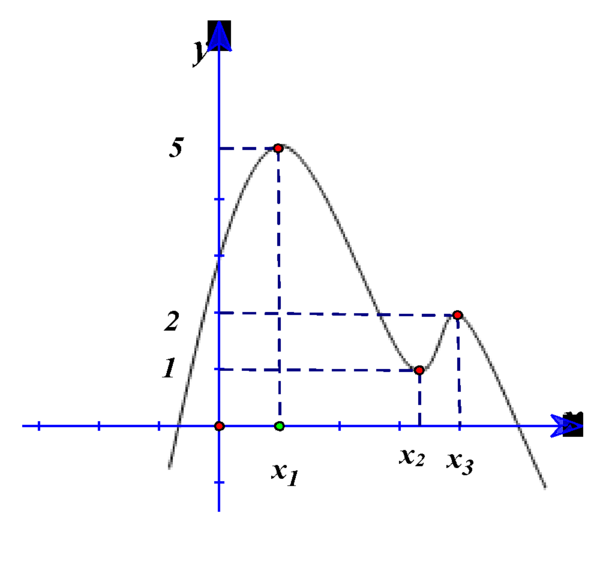
A. 1
B. 2
C. 3
D. 4
Chọn D
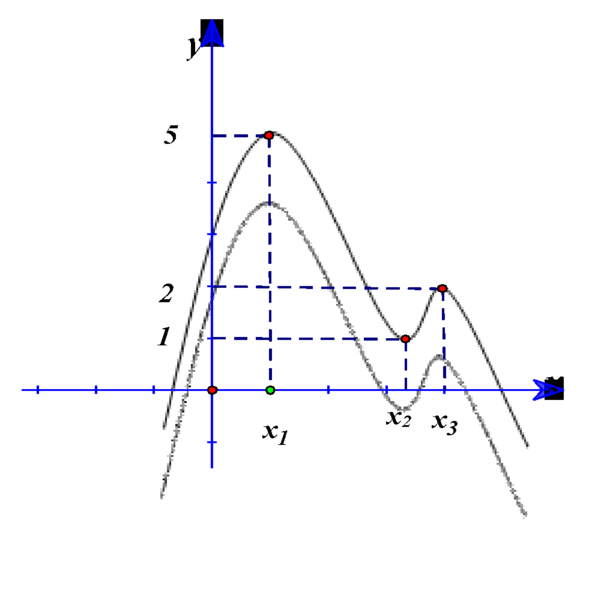
Ta có
![]() .
.
Suy ra đồ thị của hàm số y= g’(x) là phép tịnh tiến đồ thị hàm số y= f’(x) theo phương song song với trục Oy xuống dưới ![]() đơn vị.
đơn vị.
Ta có ![]() và dựa vào đồ thị của hàm số y= f’(x) , ta suy ra
và dựa vào đồ thị của hàm số y= f’(x) , ta suy ra
đồ thị của hàm số y= g’(x) cắt trục hoành tại 4 điểm.
=> Hàm số y= g( x) có 4 cực trị .
Cho hàm số y= f( x) liên tục và xác định trên R. Biết f( x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ. Xét trên ![]() , khẳng định nào sau đây đúng?
, khẳng định nào sau đây đúng?
A. Hàm số y= f( x) đồng biến trên khoảng ![]() .
.
B. Hàm số y= f( x) nghịch biến trên khoảng ![]() .
.
C. Hàm số y= f(x) nghịch biến trên khoảng - π ; - π 2 và π 2 ; π .
D. Hàm số y= f( x) đồng biến trên khoảng ![]() .
.
Chọn D
Trong khoảng ![]() đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
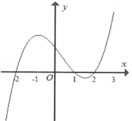
Cho hàm số y=f(x) liên tục và có đạo hàm trên R đồ thị hàm số y=f'(x) như hình vẽ bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()