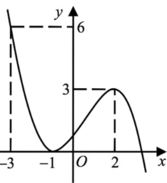
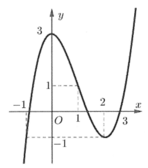
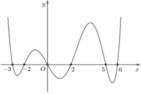
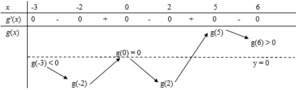
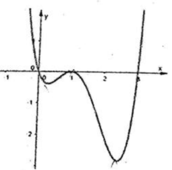
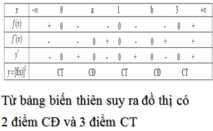
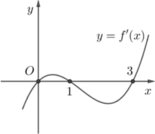
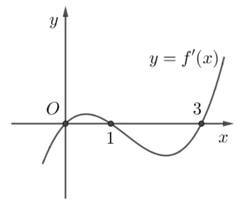
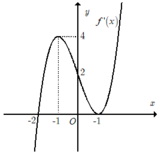
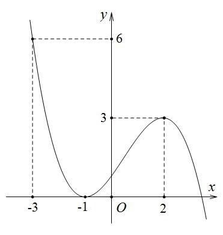
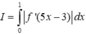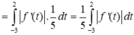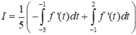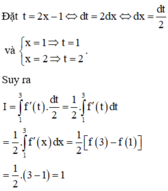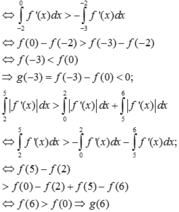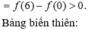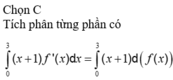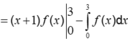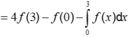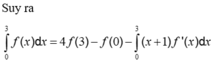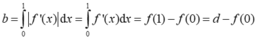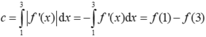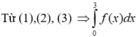Cho hàm số y = f(x) liên tục, có đạo hàm trên ![]() và có đồ thị như hình vẽ. Tích phân
I
=
∫
0
1
f
'
5
x
-
3
bằng
và có đồ thị như hình vẽ. Tích phân
I
=
∫
0
1
f
'
5
x
-
3
bằng
A. 9/5
B. 9
C. 3
D. 2