Một khối cầu có thể tích 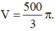 Tính diện tích S của mặt cầu tương ứng
Tính diện tích S của mặt cầu tương ứng
![]()
![]()
![]()
![]()
Một khối cầu có thể tích V = 500 3 π . Tính diện tích S của mặt cầu tương ứng
A. S = 25 π
B. S = 50 π
C. S = 75 π
D. S = 100 π
Đáp án D
Ta có V = 4 3 π R 3 = 500 3 π ⇒ R 3 = 125 ⇒ R = 5 ⇒ S = 4 π R 2 = 100 π
Trong không gian Oxyz, cho mặt cầu (S) có phương trình: x 2 + y 2 + z 2 = 4 a 2 (a > 0). Tính diện tích của mặt cầu (S) và thể tích của khối cầu tương ứng.
Trong không gian Oxyz, cho mặt cầu (S) có phương trình: x 2 + y 2 + z 2 = 4 a 2 (a > 0). Tính diện tích của mặt cầu (S) và thể tích của khối cầu tương ứng.
Mặt cầu (S) cắt mặt phẳng (Oxy) theo đường tròn (C). Xác định tâm và bán kính của (C).
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
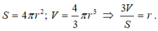
Cho một khối cầu có thể tích bằng 500 π 3 . Tính diện tích S của mặt cầu đó.
![]()
![]()
![]()
![]()
Cho một khối cầu có thể tích bằng 500 π 3 . Tính diện tích S của mặt cầu đó
A. S = 75 π .
B. S = 100 π .
C. S = 50 π .
D. S = 25 π .
Đáp án B
V = 4 3 π R 3 = 500 π 3 ⇒ R = 5 S = 4 π R 2 = 100 π
Cho một khối cầu có thể tích bằng 500 π 3 . Tính diện tích S của mặt cầu đó
A. S = 75 π
B. S = 100 π
C. S = 50 π
D. S = 25 π
I. Trắc nghiệm ( 6 điểm)
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
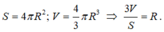
Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng bằng 4cm được thiết diện là một hình tròn có diện tích 9 π cm 2 . Tính thể tích khối cầu (S).
![]()
![]()
![]()
![]()