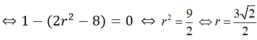Mặt phẳng (Oyz) cắt mặt cầu S : x 2 + y 2 + z 2 + 2 x - 2 y + 4 z - 3 = 0 theo một đường tròn có toạ độ tâm là:
A. (-1;0;0)
B. (0;-1;2)
C. (0;2;-4)
D. (0;1;-2)
Trong không gian hệ tọa độ Oxyz, mặt cầu (T): ( x - 2 ) 2 + ( y + 1 ) 2 + z 2 = 9 cắt mặt phẳng (Oyz) theo giao tuyến là một đường tròn có bán kính bẳng
A. 11
B. 3
C. 5
D. 7
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x + 3 ) 2 + y 2 + ( z - 2 ) 2 = m 2 + 4 . Tìm tất cả các giá trị thực của tham số m để mặt cầu (S) tiếp xúc với mặt phẳng (Oyz).
![]()
![]()
![]()
![]()
Mặt phẳng (Oyz) cắt mặt cầu (S): x 2 + y 2 + z 2 + 2 x - 2 y + 4 z - 3 = 0 theo một đường tròn có toạ độ tâm là:
A. (-1; 0; 0)
B. (0; -1; 2)
C. (0; 2; -4)
D. (0; 1; -2)
Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có bán kính bằng 2 tiếp xúc với mặt phẳng (Oyz) và có tâm nằm trên tia Ox. Phương trình của mặt cầu (S) là
A. S : x + 2 2 + y 2 + z 2 = 4
B. S : x 2 + y - 2 2 + z 2 = 4
C. S : x - 2 2 + y 2 + z 2 = 4
D. S : x 2 + y 2 + z - 2 2 = 4
Gọi ![]() là tâm của (S)
là tâm của (S)
Theo giả thiết, ta có ![]()
Vậy S : x - 2 2 + y 2 + z 2 = 4
Chọn C.
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x + 2 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 12 . Mặt phẳng nào sau đây cắt mặt cầu (S) theo giao tuyến là một đường tròn?
A. ( P 1 ) : x + y - z + 2 = 0
B. ( P 2 ) : x + y - z - 2 = 0
C. ( P 3 ) : x + y - z + 10 = 0
D. ( P 4 ) : x + y - z - 10 = 0
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x + 2 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 12 . Mặt phẳng nào sau đây cắt mặt cầu (S) theo giao tuyến là một đường tròn?
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (Oyz) cắt mặt cầu ( S ) : x 2 + y 2 + z 2 + 2 x - 2 y + 4 z - 3 = 0 theo một đường tròn có tọa độ tâm H là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : 2x - 2y + z + 3 = 0 và mặt cầu S : x - 1 2 + ( y + 3 ) 2 + z 2 = 9 và đường thẳng d : x - 2 = y + 2 1 = z + 1 2 . Cho các phát biểu sau đây:
I. Đường thẳng d cắt mặt cầu (S) tại 2 điểm phân biệt.
II. Mặt phẳng (P) tiếp xúc với mặt cầu (S)
III. Mặt phẳng (P) và mặt cầu (S) không có điểm chung
IV. Đường thẳng d cắt mặt phẳng (PA) tại 1 điểm
Số phát biểu đúng là:
A. 4
B. 1
C. 2
D. 3
Cho mặt cầu ( S ) : ( x - 2 ) 2 + y 2 + ( z + 1 ) 2 = 14 Mặt cầu (S) cắt trục Oy tại A, B. Mặt phẳng tiếp xúc với mặt cầu (S) tại B là
A. -2x + 3y + z +9 = 0
B. 2x - 3y +-z +9 = 0
C. -2x + 3y - 2z - 9 = 0
D. x - 3y + 2z - 9 = 0
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Chọn D
Gọi I (m; 0; 0) là tâm mặt cầu có bán kính R, d1, d2 là các khoảng cách từ I đến (P) và (Q).
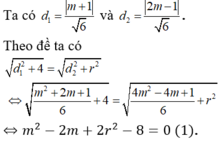
Yêu cầu bài toán tương đương phương trình (1) có đúng một nghiệm m