Tính giới hạn:lim 1 + 3 + 5 + . . . + ( 2 n + 1 ) 3 n 2 + 4 .
A. 0.
B. 1 3 .
C. 2 3 .
D. 1.
Tính giới hạn:lim 1 + 3 + 5 + . . . + ( 2 n + 1 ) 3 n 2 + 4 .
A. 0.
B. 1 3 .
C. 2 3 .
D. 1.
Tính giới hạn:lim 1 1 . 2 + 1 2 . 3 + . . . + 1 n ( 2 n + 1 ) .
A. 0
B. 1.
C. 3 2 .
D. Không có giới hạn.
Tính giới hạn:lim 1 1 . 2 + 1 2 . 3 + . . . + 1 n ( n + 1 ) .
A. 0
B. 1.
C. 3 2 .
D. Không có giới hạn.
Tính giới hạn: l i m 1 + 3 + 5 + . . . . + ( 2 n + 1 ) 3 n 2 + 4
A. 0.
B. 1/3.
C. 2/3.
D. 1.
Tính giới hạn: 1 + 3 + 5 . . . + 2 n + 1 3 n 2 + 4
A. 0
B. 1 3
C. 2 3
D. 1
Đáp án là B
l i m 1 + 3 + 5 + . . . + ( 2 n + 1 ) 3 n 2 + 4
Ta có: 1+3 + 5+ .... + (2n +1) là tổng của n +1 số hạng 1 cấp số cộng có u 1 = 1 và công sai d =2.
Nên 1+ 3 + 5+ .. + (2n+1) = ( n + 1 ) 2 . 2 . 1 + ( n + 1 - 1 ) . 2 = n + 1 2
l i m 1 + 3 + 5 + . . . + ( 2 n + 1 ) 3 n 2 + 4 = l i m n + 1 2 3 n 2 + 4
= l i m n 2 + 2 n + 1 3 n 2 + 4 = l i m 1 + 2 n + 1 n 2 3 + 4 n 2 = 1 3
Tính giới hạn I = lim 2 n ( 3 - n ) + 1 1 + 3 + 5 + . . + ( 2 n - 1 ) .
A. I = 2
B. I = 1
C. I = -2
D. I = -3
Tính giới hạn: l i m 1 + 3 + 5 + . . . + ( 2 n + 1 ) 3 n 2 + 4 .
A. 0
B. 1 3
C. 2 3
D. 1
- Ta có : 1 + 3 + 5 + ... + (2n + 1) là tổng của cấp số cộng có n số hạng với u1 = 1 và công sai d = 2
- Do đó:
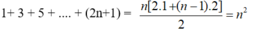
- Suy ra:
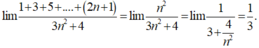
Chọn B
Tính giới hạn: l i m 1 + 3 + 5 + . . . + ( 2 n + 1 ) 3 n 2 + 4
A. 0
B. 1 3
C. 2 3
D. 1
- Ta có : 1 + 3 + 5 + ... + (2n + 1) là tổng n số hạng của 1 cấp số cộng với số hạng đầu u 1 = 1 và công sai d = 2
- Do đó:
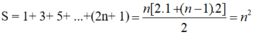
- Suy ra:
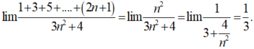
Chọn B.
4. Tính giới hạn \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x^2+1}-x-1}{2x^2-x}_{ }\)
5. Tính giới hạn:
a) \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{x^2-4}_{ }\)
b) \(\lim\limits_{x\rightarrow3^-}\dfrac{x+3}{x-3}_{ }\)
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x^2+1}-\left(x+1\right)}{2x^2-x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{x^2+1}-\left(x+1\right)\right)\left(\sqrt{x^2+1}+x+1\right)}{x\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-2x}{x\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-2}{\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)
\(=\dfrac{-2}{\left(0-1\right)\left(\sqrt{1}+1\right)}=1\)
a. \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{x^2-4}=\lim\limits_{x\rightarrow2}\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\lim\limits_{x\rightarrow2}\dfrac{1}{x+2}=\dfrac{1}{4}\)
b. \(\lim\limits_{x\rightarrow3^-}\dfrac{x+3}{x-3}=\lim\limits_{x\rightarrow3^-}\dfrac{-x-3}{3-x}\)
Do \(\lim\limits_{x\rightarrow3^-}\left(-x-3\right)=-6< 0\)
\(\lim\limits_{x\rightarrow3^-}\left(3-x\right)=0\) và \(3-x>0;\forall x< 3\)
\(\Rightarrow\lim\limits_{x\rightarrow3^-}\dfrac{-x-3}{3-x}=-\infty\)