Tính mô đun của số phức z thỏa mãn z 2 + 3 i + i = z .
A. 1 10
B. 3
C. 10
D. 3
Cho số phức z thỏa mãn z(2-i)+13i=1. Tính mô đun của số phức z
A. | z | = 34
B. | z | = 34
C. | z | = 34 3
D. | z | = 5 34 3
Cho số phức z thỏa mãn z(2-i)+13i=1. Tính mô đun của số phức z.
A. z = 34
B. z = 34
C. z = 34 3
D. z = 5 34 3
Đáp án B
Phương pháp
Từ giả thiết ta biến đổi để tìm được công thức của z. Dùng định nghĩa để tìm z
Lời giải chi tiết.
Ta có:
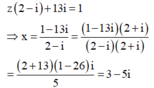
Do đó ![]()
Cho số phức z thỏa mãn z(2-i) + 13i = 1. Tính mô đun của số phức z.
A. |z| = 34
B. |z| = 34
C. |z| = 5 34 3
D. |z| = 34 3
Cho số phức z thỏa mãn z(2-i) + 13i = 1. Tính mô đun của số phức z.
A. |z| = 34
B. |z| = 34
C. |z| = 5 34 3
D. |z| = 34 3
Cho số phức z thỏa mãn z ( 2 - i ) + 12 i = 1 . Tính mô đun của số phức z.
![]()
![]()
![]()
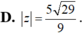
Cho số phức z thỏa mãn z(2-i)+13i = 1 Tính mô đun của số phức z.
![]()
![]()

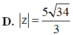
Cho số phức z thỏa mãn z(2-i)+12i=1. Tính mô đun của số phức
A. |z|=29
B. z = 29
C. z = 29
D. z = 5 29 9
Cho số phức z thỏa mãn ( 1+ i) z + 2z = 2. Tính mô-đun của số phức w = z + 2/5 - 4/5i.
A. 1.
B. 2.
C. 2
D. 3
Chọn C.
Đặt z = a+ bi.
Theo đề ra ta có: ( 3 + i) z = 2
Hay ( 3 + i)( a + bi) = 2
Suy ra: 3a - b + ( 3b + a) i = 2
![]()
nên z = 3/5 - 1/5i.
Khi đó w = 3/5 - 1/5i + 2/5 - 4/5 i = 1 - i.
Vậy ![]()
Số phức thỏa mãn phương trình z + 3 z ¯ = ( 2 + i ) 3 ( 2 - i ) Mô đun của số phức w = z + 10 i là
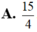
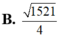
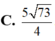
![]()
Cho số phức z thỏa mãn z 2 − i + 13 i = 1. Tính mô đun của số phức z
A. z = 34
B. z = 34
C. z = 5 34 3
D. z = 34 3
Đáp án A
P T ⇔ z = 1 − 13 i 2 − i = 3 − 5 i ⇒ z = 3 2 + − 5 2 = 34 .