Có bao nhiêu hạng tử là số nguyên trong khai triển 3 + 5 4 124 ?
A. 32
B. 31
C. 33
D. 30
Có bao nhiêu số hạng là số nguyên trong khai triển của biểu thức 3 3 + 5 5 2019 ?
![]()
![]()
![]()
![]()
Có bao nhiêu số hạng là số nguyên trong khai triển của biểu thức 3 3 + 5 5 2019
A. 403
B. 134
C. 136
D. 135
Trong khai triển biểu thức F = 3 + 2 3 9 thành tổng của 10 số hạng, hỏi số hạng là số nguyên có giá trị lớn nhất trong các số hạng là số nguyên của khai triển này.
A. 8
B. 4536
C. 4528
D. 4520
Có tất cả bao nhiêu số hạng mà luỹ thừa của x nguyên trong khai triển 2 x - x 3 9 ?
A. 3.
B. 1.
C. 4.
D. 2.
Có tất cả bao nhiêu số hạng mà luỹ thừa của x nguyên trong khai triển 2 x - x 3 9
A. 3
B. 1
C. 4
D. 2
Có tất cả bao nhiêu số hạng mà luỹ thừa của x nguyên trong khai triển 2 x - x 3 9 ?
A. 3.
B. 1.
C. 4.
D. 2.
1.nếu n là số nguyên dương sao cho 2n có 28 ước số dương và 3n có 30 ước số dương. Thì số 6n có bao nhiêu ước số dương 2.cho biểu thức (2x+1/x^2)^n với n là số nguyên dương a) tìm n để số hạng thứ 3 trong triển khai theo số mũ giảm dần của 2x( của biểu thức trên) không chữa x và tính số hạng ấy b) với giá trị nào của x thì số hạng tìm được ở câu a) bằng số hạng thứ 2 trong triển khai theo số mũ giảm dần của x^3 của biểu thức ( 1+x^3)^30
Biết rằng khi khai triển nhị thức Niutơn x + 1 2 x 4 n = a 0 x n + a 1 x n - 1 1 x 4 + a 2 x n - 2 1 x 4 2 + + a 3 x n - 3 1 x 4 3 . . . (với n là số nguyên lớn hơn 1) thì ba số a 0 , a 1 , a 2 theo thứ tự lập thành một cấp số cộng. Hỏi trong khai triển trên, có bao nhiêu số hạng mà lũy thừa của x là một số nguyên.
A. 1
B. 2
C. 3
D. 4
Biết rằng khi khai triển nhị thức Niutơn x + 1 2 x 4 n = a 0 x n + a 1 x n - 1 . 1 x 4 + a 2 x n - 2 . 1 x 4 2 + a 3 x n - 3 . 1 x 4 3 . . . (với n là số nguyên lớn hơn 1) thì ba số a 0 , a 1 , a 2 theo thứ tự lập thành một cấp số cộng. Hỏi trong khai triển trên, có bao nhiêu số hạng mà lũy thừa của x là một số nguyên.
A. 1
B. 2
C. 3
D. 4
Đáp án C
Yêu cầu bài toán 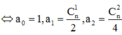 lập thành cấp số cộng
lập thành cấp số cộng
Khi và chỉ khi 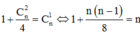
![]()
Do đó, số hạng tổng quát của khai triển là 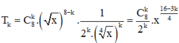
Số hạng mà lũy thừa của x là số nguyên ứng với ![]() mà
mà ![]()
Suy ra k = {0;4;8} → Có 3 số hạng lũy thừa của x là số nguyên