Trong không gian Oxyz, cho mặt phẳng ( P ) : m x + ( 2 m + 1 ) y - z - 4 m + 2 = 0 và A(1;2;0). Khi khoảng cách từ A đến mặt phẳng (P) lớn nhất thì hình chiếu vuông góc của A lên (P) là H(a;b;c). Giá trị của a + b + c bằng
A. 5
B. 6
C. 7
D. 8
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x + 2 y - z - 1 = 0 , (Q): 3x-(m+2)y+(2m-1)z+3=0. Tìm m để hai mặt phẳng (P), (Q) vuông góc với nhau.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) = x - y + z - 5 = 0. Tính khoảng cách d từ M(1 ; 2 ; 1) đến mặt phẳng ( P ) được:
A. d = 15 3
B. d = 12 3
C. d = 5 3 3
D. d = 4 3 3
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( P ) : x + y – z – 4 = 0 và điểm M (1;–2;-2). Tọa độ điểm N đối xứng với điểm M qua mặt phẳng (P) là
A. N (3;4;8)
B. N (3;0;–4)
C. N (3;0;8)
D. N (3;4;–4)
Trong không gian Oxyz, cho ba mặt phẳng (P), (Q), (R) lần lượt có phương trình là ( m 2 + m)x - (m + 2)y + z = 0; x + y + z = 0; 2x + y - z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R)?
A. m = 1
B. m = -1
C. m = -3/2
D. m = -3/2 hoặc m = -1
Đáp án A
Ta có:
![]()
Mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R) khi và chỉ khi
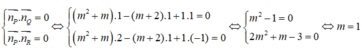
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x-2y+z+14=0. Gọi M ( a ; b ; c ) là điểm thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) lớn nhất. Tính T = a + b + c .
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu (S): (x - 2) 2 + (y + 1) 2 + (z + 2) 2 = 4 và mặt phẳng (P): 4x - 3y + m = 0. Với những giá trị nào của m thì mặt phẳng (P) và mặt cầu (S) có đúng một điểm chung?
A. m=-1
B. m=9 hoặc m=-31
C. m=1 hoặc m=21
D. m=-1 hoặc m=-21
Đáp án D
Mặt cầu (S) có tâm I(2;-1;-2) và có bán kính R=2. Mặt phẳng (P) và mặt cầu (S) có đúng một điểm chung khi và chỉ khi (P) tiếp xúc với (S), từ đó ta được:
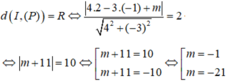
Trong không gian hệ tọa độ Oxyz, cho đường thẳng x - 2 1 = y - 1 = z + 1 - 2 và mặt phẳng P : 3 m - 1 x - m + 1 y - 1 + 3 m 2 z + 2 = 0 . Tìm m để d ⊥ P
A. m = 1
B. m = -1
C. m = 3
D. m = -3
Chọn A.
Phương pháp: Điều kiện để đường thẳng vuông góc với mặt phẳng là véc tơ chỉ phương của đường thẳng và véc tơ pháp tuyến của mặt phẳng cùng phương.

Trong không gian Oxyz, cho hai mặt phẳng ( P ) : 2 x - m y - 4 z - 6 + m = 0 v à ( Q ) : ( m + 3 ) x + y + ( 5 m + 1 ) z - 7 = 0 . Tìm m để hai mặt phẳng (P) và (Q) trùng nhau
A. m = - 6 5
B. m = 1
C. m = -1
D. m = 4
Chọn C.
Để hai mặt phẳng (P) và (Q) trùng nhau khi và chỉ khi:
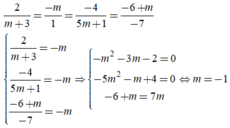
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng α : x + y - z + 1 = 0 v à β : - 2 x + m y + 2 z - 2 = 0 . Tìm m để mặt phẳng (α) song song với mặt phẳng (β).
A. m = 2
B. m = 5
C. Không tồn tại
D. m = -2
Trong không gian với hệ tọa độ Oxyz cho điểm M(1;4;2) và mặt phẳng ( α ) : x + y + z - 1 = 0 . Tọa độ điểm M’ đối xứng với điểm M qua mặt phẳng (α) là
A. M’(0;-2;-3)
B. M’(-3;-2;0)
C. M’(-2;0;-3)
D. M’(-3;0;-2)