Trên mặt phẳng phức, tập hợp các số phức z = x + y i x , y ∈ ℝ thỏa mãn z + 2 + i = z ¯ - 3 i là đường thẳng có phương trình
A. y = x + 1
B. y = - x + 1
C. y = - x - 1
D. y = x - 1
Những câu hỏi liên quan
Xét các số phức zx+yi
x
,
y
∈
R
có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình (C):
x
-
1
2
+
y
-
2...
Đọc tiếp
Xét các số phức z=x+yi x , y ∈ R có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình (C): x - 1 2 + y - 2 2 = 4 . Tập hợp các điểm biểu diễn của số phức là w = z + z ¯ + 2 i
Xét các số phức
z
x
+
y
i
x
,
y
∈
ℝ
có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình
C
:
x
-
1
2
+
y
-...
Đọc tiếp
Xét các số phức z = x + y i x , y ∈ ℝ có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình C : x - 1 2 + y - 2 2 = 4 . Tập hợp các điểm biểu diễn của số phức là w = z + z ¯ + 2 i
A. Đường thẳng
B. Đoạn thẳng.
C. Điểm
D. Đường tròn.
Xét các số phức
z
x
+
y
i
x
,
y
∈
ℝ
có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình
(
C
)
:
x
-
1
2
+
y
-...
Đọc tiếp
Xét các số phức z = x + y i x , y ∈ ℝ có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình ( C ) : x - 1 2 + y - 2 2 = 4 . Tập hợp các điểm biểu diễn của số phức là w = z + z ¯ + 2 i
A. Đường thẳng
B. Đoạn thẳng
C. Điểm
D. Đường tròn
Số phức z = x + y i x , y ∈ ℝ có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình
( C ) : x - 1 2 + y - 2 2 = 4 ⇒ - 1 ≤ x ≤ 3
w = z + z ¯ + 2 i = x + y i + x - y i + 2 i = 2 x + 2 i
Tọa độ điểm biểu diễn số phức w là M ( x ; 2 ) , x ∈ - 1 ; 3
Vậy, tập hợp các điểm biểu diễn của số phức là w là đoạn thẳng AB với A(-1;2),B(3;2)
Chọn đáp án B.
Đúng 0
Bình luận (0)
Trên mặt phẳng phức tập hợp các số phức z = x + yi thỏa mãn |z + 2 - i| = | z ¯ - 3i| là đường thẳng có phương trình
A. y = x + 1
B. y = -x + 1
C. y = -x - 1
D. y = x - 1
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn số phức
z
x
+
i
y
,
x
,
y
∈
ℝ
thỏa mãn điều kiện
z
2
. A. Đường tròn
x
2
+
y
2
4
. B. Đường thẳng
x
2
. C...
Đọc tiếp
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z = x + i y , x , y ∈ ℝ thỏa mãn điều kiện z = 2 .
A. Đường tròn x 2 + y 2 = 4 .
B. Đường thẳng x = 2 .
C. Đường thẳng y = 2
D. Hợp hai đường thẳng x = 2, y = 2 .
Đáp án A
z = 2 ⇔ x 2 + y 2 = 2 ⇔ x 2 + y 2 = 4 .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ, tập hợp các điểm
M
x
;
y
biểu diễn của số phức
z
x
+
y
i
x
;
y
∈
ℝ
thỏa mãn
z
+
1
+
3
i
z
-
2
-...
Đọc tiếp
Trong mặt phẳng tọa độ, tập hợp các điểm M x ; y biểu diễn của số phức z = x + y i x ; y ∈ ℝ thỏa mãn z + 1 + 3 i = z - 2 - i là
A. Đường tròn tâm O bán kính R = 1
B. Đường tròn đường kính AB với A - 1 ; - 3 và B 2 ; 1
C. Đường trung trực của đoạn thẳng AB với A - 1 ; - 3 và B 2 ; 1
D. Đường thẳng vuông góc với đoạn AB tại A với A A - 1 ; - 3 , B 2 ; 1
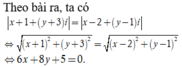
Phương trình đường trung trực của AB là: 6x + 8y + 5 = 0
Vậy tập hợp các điểm M(x;y) biểu diễn số phức z và thỏa mãn yêu cầu bài toán là đường thẳng trung trực của đoạn AB với A - 1 ; - 3 và B 2 ; 1
Chọn C.
Đúng 0
Bình luận (0)
Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho
z
−
i
z
+
i
là số thực. A. Đường tròn phương trình
x
2
+
y
2
1
bỏ đi điểm (0;−1). B. Trục tung bỏ đi điểm (0;−1). C. Hyperbol phương trình...
Đọc tiếp
Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho z − i z + i là số thực.
A. Đường tròn phương trình x 2 + y 2 = 1 bỏ đi điểm (0;−1).
B. Trục tung bỏ đi điểm (0;−1).
C. Hyperbol phương trình x 2 − y 2 = − 1 bỏ đi điểm (0;−1).
D. Trục hoành bỏ đi điểm (0;1).
Đáp án B
Gọi z = x + i y ; x , y ∈ ℝ .
z − i z + i = x + i y − 1 x + i y + 1 = x + i y − 1 x − i y + 1 x 2 + y + 1 2 = x 2 + y 2 − 1 + i x y − 1 − x y + 1 x 2 + y + 1 2 = x 2 + y 2 − 1 x 2 + y + 1 2 + i − 2 x x 2 + y + 1 2 .
z − i z + i là số thực ⇔ − 2 x x 2 + y + 1 2 = 0 ⇔ x = 0 x ≠ 0 ; x ≠ − 1 là trục tung bỏ đi điểm (0;−1).
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn: |z - 1 + i| = 2. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:
A. Một đường thẳng.
B. Một đường Parabol.
C. Một đường tròn có bán kính bằng 2.
D. Một đường tròn có bán kính bằng 4.
Đáp án C
Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
Số phức z1 được biểu diễn bởi điểm A(1;-1).
Em có: |z - 1 + i| = 2 => MA = 2
Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: 
Cách 2: Đặt 
. Số phức z được biểu diễn bởi điểm M(x;y).
Em có:
Vậ tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình: 
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn:
z
−
1
+
i
2
. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là: A. Một đường thẳng B. Một đường Parabol C. Một đường tròn có bán kính bằng 2 D. Một đường tròn có bán kính bằng 4
Đọc tiếp
Cho số phức z thỏa mãn: z − 1 + i = 2 . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:
A. Một đường thẳng
B. Một đường Parabol
C. Một đường tròn có bán kính bằng 2
D. Một đường tròn có bán kính bằng 4
Đáp án C
Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
Số phức z 1 được biểu diễn bởi điểm A(1;-1).
Em có: z − 1 + i = 2 ⇒ MA = 2 .
Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: x − 1 2 + y + 1 2 = 4 .
Cách 2: Đặt z = x + yi , x ; y ∈ ℝ . Số phức z được biểu diễn bởi điểm M(x;y).
Em có:
z − 1 + i = 2 ⇔ x − 1 + y + 1 i = 2 ⇔ x − 1 2 + y + 1 2 = 2 ⇔ x − 1 2 + y + 1 2 = 4
Vậy tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình:
x − 1 2 + y + 1 2 = 4 .
Đúng 0
Bình luận (0)