Tập nghiệm của bất phương trình ln x 2 < 0 là
A. (-1,1)
B. (0,1)
C. (-1,0)
D. ( - 1 , 1 ) \ { 0 }
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Cho hàm số f ( x ) = l n ( x 2 - 2 x + 3 ) . Tập nghiệm của bất phương trình f'(x)>0 là
A. ( 2 ; + ∞ ) .
B. ( - 1 ; + ∞ ) .
C. ( - 2 ; + ∞ ) .
D. ( 1 ; + ∞ ) .
Tìm tập nghiệm của bất phương trình ( 2 x - 7 ) ln ( x + 1 ) > 0
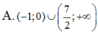
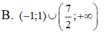
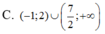
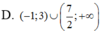
Tập nghiệm của bất phương trình 2 x 2 − 4 − 1 . ln ( x 2 ) < 0 là
A. S = [ 1 ; 2 ] .
B. S = { 1 ; 2 } .
C. S = ( 1 ; 2 ) .
D. S = ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Đáp án D.
Cách 1: Tư duy tự luận
Điều kiện: x 2 > 0 ⇔ x ≠ 0.
Bất phương trình
( 2 x 2 − 4 − 1 ) . ln ( x 2 ) < 0 ⇔ 2 x 2 − 4 − 1 < 0 ln ( x 2 ) > 0 2 x 2 − 4 − 1 > 0 ln ( x 2 ) < 0 ⇔ x 2 − 4 < 0 x 2 > 1 x 2 − 4 > 0 x 2 < 1 ( L )
⇔ ( x − 2 ) ( x + 2 ) < 0 ( x − 1 ) ( x + 1 ) > 0 ⇔ − 2 < x < 2 x > 1 x < − 1 ⇔ 1 < x < 2 − 2 < x < − 1
Vậy tập nghiệm của bất phương trình là S = ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Cách 2: Sử dụng máy tính cầm tay
Nhập vào màn hình biểu thức 2 x 2 − 4 − 1 . ln ( X 2 ) và CALC với X = − 2 ; − 1 ; 1 ; 2.

Ta xét dấu của biểu thức 2 X 2 − 4 − 1 . ln ( X 2 ) trên mỗi khoảng ( − ∞ ; − 2 ) , ( − 2 ; − 1 ) , ( − 1 ; 1 ) , ( 1,2 ) , ( 2 ; + ∞ ) .
Tiếp tục dùng CACL:

Vậy
( 2 x 2 − 4 − 1 ) . ln ( x 2 ) < 0 ⇔ x ∈ ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Tập nghiệm của bất phương trình 2 x 2 − 4 − 1 . ln ( x 2 ) < 0 là
A. S = [ 1 ; 2 ] .
B. S = { 1 ; 2 } .
C. S = ( 1 ; 2 ) .
D. S = ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Tìm tập nghiệm của bất phương trình ln x 2 < 0
A. S = (-1;1)
B. S = (0;1)
C. S = (-1;0)
D. S = (-1;1)\{0}
Điều kiện: ![]()
Bất phương trình ![]()
Đối chiếu điều kiện ta được tập nghiệm S = (-1;1)\{0}
Chọn D.
Tìm tập nghiệm S của bất phương trình ln x 2 < 0
A. S = (-1; 1)
B. S = (0; 1)
C. (-1; 0)
D. ( - 1 ; 1 ) \ { 0 }
Đề thi môn toán 8 học kì 2
Câu 1 Giải các phương trình sau:
a) x-2=0, b) (x+5)(2x-7)=0. =c) . 5x/x+2 =4
Câu 2. a) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: a )2x-6>_(hoặc bằng)=0.
b) Cho a<b. Chứng minh
: -3a+7> -3b+7
Câu 3 (1,0 điểm). Giải bài toán bằng cách lập phương trình:
Một người đi ôtô từ huyện Cao Lãnh đến huyện Thanh Bình với vận tốc 40 km/h. Sau khi đi đến huyện Thanh Bình người đó giải quyết công việc hết 30 phút .rồi quay về huyện Cao Lãnh với vận tốc 50 km/h. Biết thời gian cả đi và về hết 2 giờ 18 phút (kể cả thời gian giải quyết công việc). Tính quãngđường từ huyện Cao Lãnh đến huyện Thanh Bình.
Câu 4 (1,0 điểm). Một container chứa hàng có kích thước như sau: dài 6m, rộng 2,4m; cao 2,6m. Tínhthể tích của thùng container.
Câu 5 (3,0 điểm). Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Kẻ AH vuông góc với BC tại H
a) Chứng minh: tamgiácHBA đồng dạng với tamgiácABC.
b) Chứng minh: AB2 =BH.BC
c) Tính độ dài cạnh BC, BH.
Phân giác của góc ACB cắt AH tại E và cắt AB tại D. Tính tỉ số diện tích của tam giác ACD và tam giácHCE.
Giúp mình với mn ơii .mai mình nộp r
GIUP VOI MOI NGUOI OI .CUU EM VOIIIIII !!!!!!!!!!
câu 1
a) 5x(x-2)=0 =>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
b)(x+5)(2x-7)=0 =>\(\left[{}\begin{matrix}x+5=0\\2x-7=0\end{matrix}\right.\)=>\(\left[{}\begin{matrix}x=-5\\x=\dfrac{7}{2}\end{matrix}\right.\)
Tập nghiệm của bất phương trình - 3 x 2 + x + 4 ≥ 0 là:
A. S = ∅
B. S = (-∞; -1] ∪ [4/3; +∞]
C. S = [-1; 4/3]
D. S = (-∞; +∞)