Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho đa giác đều có 20 đỉnh. Số tam giác được tạo nên từ các đỉnh này là
A. A 20 3
B. 3 ! C 20 3
C. 10 3
D. C 20 3
Cho đa giác đều (H) có 20 cạnh. Xét tam giác có 3 đỉnh được lấy từ các đỉnh của (H). Hỏi có bao nhiêu tam giác có đúng1 cạnh là cạnh của (H)
A. 320
B. 360
C. 380
D. 400
• Chọn một cạnh của đa giác (H) làm cạnh của tam giác nên có 20 cách.
• Chọn một đỉnh (để ghép với cạnh đã chọn ở bước trên tạo thành tam giác thỏa mãn bài toán) nên có 16 cách chọn (bỏ2 đỉnh thuộc cạnh đã chọn và 2 đỉnh liền kề hai bên cạnh đã chọn).
Vậy số tam giác cần tìm là 20 x 16 = 320.
Chọn A.
Cho đa giác đều (P) có 20 đỉnh. Lấy tùy ý 3 đỉnh của (P), tính xác suất để 3 đỉnh lấy được tạo thành tam giác vuông không có cạnh nào là cạnh của (P).
A. 3/38
B. 7/114
C. 7/57
D. 5/114
Chọn C.
Chọn ngẫu nhiên 3 đỉnh của đa giác có: C 20 3 = 1140 cách chọn.
Đa giác đều có 20 đỉnh có 10 đường chéo đi qua tâm đa giác mà cứ 2 đường chéo tại thành 1 hình chữ nhật và 1 hình chữ nhật tạo thành 4 tam giác vuông.
Trong 10 đường chéo đi qua tâm ta trừ đi 10 hình chữ nhật chứa cạnh của (P)
Do đó số tam giác vuông không có cạnh nào của (P) là: 4 C 10 2 - 10 = 140 tam giác.
Vậy xác suất cần tìm là: P = 140/1140 = 7/57
Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
A . 3 38
B . 7 114
C . 7 57
D . 5 114
Chọn C
Đa giác đều nội tiếp một đường tròn tâm O. Lấy ngẫu nhiên 3 đỉnh có C 20 3 cách.
Để 3 đỉnh là 3 đỉnh một tam giác vuông không có cạnh nào là cạnh của đa giác đều thực hiện theo các bước:
Lấy một đường kính qua tâm đường tròn có 10 cách ta được 2 đỉnh.
Chọn đỉnh còn lại trong 20 - 2 - 4 = 14 đỉnh (loại đi 2 đỉnh thuộc đường kính và 4 đỉnh gần ngay đường kính đó) cách.
Vậy có tất cả 10.14 = 140 tam giác thoả mãn.
Xác suất cần tính bằng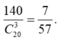 
Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
A. 3 38
B. 7 114
C. 7 57
D. 5 114
Một hình đa giác đều gồm 20 cạnh. Hỏi có thể lập được a. Bao nhiêu hình chữ nhật từ các định của đa giác trên? b. Bao nhiều hình tam giác từ các đỉnh của tam giác trên? c. Bao nhiêu đường chéo?
tham khảo
Đa giác đều có 20 cạnh thì sẽ có tất cả 10 đường chéo đi qua tâm của đa giác.
Một hình chữ nhật được tạo thành từ 2 đường chéo đi qua tâm, suy ra số hình chữ nhật được tạo thành là C210C102
Hình vuông được tạo thành từ 2 đường chéo vuông góc nhau, ta có tất cả 5 cặp đường chéo vuông góc nhau, suy ra có tất cả 5 hình vuông.
Vậy có 40 hình chữ nhật (không phải hình vuông) được tạo thành.
Cho đa giác đều 100 đỉnh nội tiếp một đường tròn. Số tam giác tù được tạo thành từ 3 trong 100 đỉnh của đa giác là
Cho đa giác đều 100 đỉnh nội tiếp một đường tròn. Số tam giác tù được tạo thành từ 3 trong 100 đỉnh của đa giác là
A. 44100.
B. 78400.
C. 117600.
D. 58800.
