Cho hàm số y=f(x) xác định và liên tục trên ℝ , có bảng biến thiên như hình bên. Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A. (-3;2)
B. - ∞ ; 0
C. 1 ; + ∞
D. (0;1)
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. 1 ; + ∞
B. - 1 ; 0
C. - ∞ ; 1
D. 0 ; 1
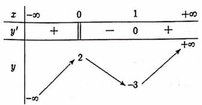
Cho hàm số y = f(x) xác định và liên tục trên ℝ và có bảng biến thiên như hình bên. Khẳng định nào sau đây sai?
A. M(0;-3) là điểm cực tiểu của hàm số
B. Đồ thị hàm số có hai điểm cực đại và một điểm cực tiểu
C. f(2) được gọi là giá trị cực đại của hàm số
D. x 0 = 2 được gọi là điểm cực đại của hàm số
Đáp án A
M(0;-3) là điểm cực tiểu của đồ thị hàm số. Khẳng định A sai.
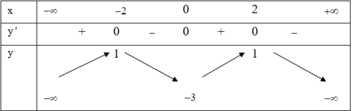
Cho hàm số y = f(x) xác định trên ℝ \ 1 , liên tục trên các khoảng xác định của nó và có bảng biến thiên như hình vẽ:
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có 3 tiệm cận.
B. Phương trình f(x) = m có 3 nghiệm thực phân biệt thì m ∈ 1 ; 2 .
C. Giá trị lớn nhất của hàm số là 2.
D. Hàm số đồng biến trên - ∞ ; 1 .
Đáp án B.
Đồ thị hàm số có 2 tiệm cận, 1 tiệm cận đứng, 1 tiệm cận ngang.
Phương trình f(x) = m có 3 nghiệm thực phân biệt thì m ∈ 1 ; 2 .
Phương án D bị gián đoạn bởi tập xác định.
Phương án C sai vì đồ thị hàm số có dáng điệu tiến đến vô cùng.
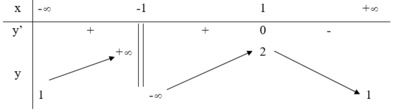
Cho hàm số y = f ( x ) xác định trên ℝ \ { - 1 } liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau :
Khẳng định nào dưới đây sai ?
A. Hàm số đồng biến trên khoảng ( - ∞ ; 1 )
B. Giá trị lớn nhất của hàm sốy=f(x) trên khoảng ( - 1 ; + ∞ ) bằng 3.
C. Hàm số đạt cực đại tại x=1
D. Đồ thị hàm số y=f(x) có 3 đường tiệm cận.
Đáp án A
Vì hàm số không xác định tại x=-1 nên hàm số đồng biến trên ( - ∞ ; - 1 ) ; ( - 1 ; 1 ) .
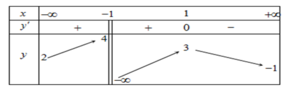
Cho hàm số y = f ( x ) xác định trên ℝ \ 1 liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
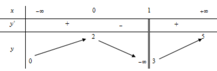
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại x=0.
B. Giả trị cực tiểu của hàm số là y C T = 3 .
C. Giá trị cực đại của hàm số là y C D = 5 .
D. Hàm số đồng biến trên khoảng 0 ; + ∞ .
Cho hàm số y=f(x) xác định trên ℝ \ − 1 ; 1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
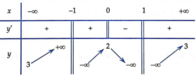
Khẳng định nào sau đây là khẳng định sai?
A. Đồ thị hàm số có hai tiệm cận đứng là các đường thẳng x=1 và x=-1
B. Đồ thị hàm số có tiệm cận ngang là đường thẳng y=3
C. Hàm số không có đạo hàm tại x=0 nhưng vẫn đạt cực trị tại x=0
D. Hàm số đạt cực tiểu tại điểm x=1
Đáp án D.
Quan sát bảng biến thiên, ta thấy:
lim x → − 1 − y = + ∞ ; lim x → − 1 + y = − ∞ lim x → 1 − y = − ∞ ; lim x → 1 + y = − ∞ → Đồ thị hàm số có hai đường tiệm cận đứng là x = − 1 và x = 1 . A đúng.
lim x → − ∞ y = 3 ; lim x → + ∞ y = 3 → Đồ thị hàm số có tiệm cận ngang là đường thẳng . B đúng.
Hàm số không có đạo hàm tại điểm , tuy nhiên vẫn đạt giá trị cực đại y=2 tại x=0 . C đúng.
Hàm số không đạt cực trị tại điểm x=1 . D sai.
Cách 1: Tư duy tự luận
Do π > 1 nên π a > π = π 1 ⇔ a > 1 . Vậy A đúng.
Do a > 1 nên a 5 < a 3 ⇔ 5 < 3 (hiển nhiên). Vậy B đúng.
Do e > 1 nên e a > 1 ⇔ e 0 ⇔ a > 0 . Vậy C đúng.
Do a > 1 nên a − 3 > a 2 ⇔ − 3 > 2 (vô lý). Vậy D sai.
Cách 2: Sử dụng máy tính cầm tay
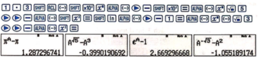
Như vậy nếu a > 1 thì a − 3 < a 2 . Đáp án D sai.
Cho hàm số y=f’(x) liên tục và có đạo hàm trên ℝ đồ thj hàm số y=f’(x) như hình vẽ bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
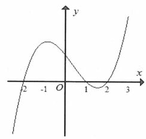
A. - ∞ ; - 2
B. - 1 ; 1
C. 2 ; + ∞
D. - ∞ ; - 1
Hàm số nghịch biến nếu f’(x)<0 Quan sát đồ thị y=f’(x), chọn đáp án A. Chọn A
Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là sai ?
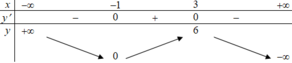
A. f(x) nghịch biến trên khoảng - ∞ ; - 1
B. f(x) đồng biến trên khoảng (0;6)
C. f(x) nghịch biến trên khoảng 3 ; + ∞
D. f(x) đồng biến trên khoảng - 1 ; 3
Đáp án là B
Trên khoảng (0;6) hàm số chứa khoảng (0;3) đồng biến và (3;6) nghịch biến. Nên đáp án B sai
Cho hàm số f(x) có đạo hàm liên tục trên ℝ . Bảng biến thiên của hàm số f’(x) trên đoạn [-1;3] như hình
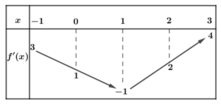
Hàm số g x = f 1 - x 2 + x nghịch biến trên khoảng nào trong các khoảng sau ?
A. (-4;-2)
B. (-2;0)
C. (0;2)
D. (2;4)
Ta có ![]()
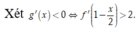
= TH1: ![]() Do đó hàm số nghịch biến trên (-4;-2)
Do đó hàm số nghịch biến trên (-4;-2)
= TH2: ![]() nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
Vậy hàm số 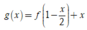 nghịch biến trên (-4;-2)
nghịch biến trên (-4;-2)
Chọn A.