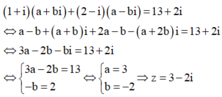Có bao nhiêu số phức z thỏa mãn: z - i = 2 và z 2 là số thuần ảo
A. 3
B. 1
C. 4
D. 2
Những câu hỏi liên quan
Có bao nhiêu số phức thỏa mãn
z
-
2
+
3
i
z
+
i
và
z
+
2
i
+
z
-
2
i
8
A. 0 B. 1...
Đọc tiếp
Có bao nhiêu số phức thỏa mãn z - 2 + 3 i = z + i và z + 2 i + z - 2 i = 8
A. 0
B. 1
C. 2
D. 3
Có bao nhiêu số phức z thỏa mãn các điều kiện
z
-
2
+
i
2
v
à
(
z
+
i
)
2
là số thuần ảo?
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn các điều kiện z - 2 + i = 2 v à ( z + i ) 2 là số thuần ảo?
Có bao nhiêu số phức z thỏa mãn
z
-
i
2
v
à
z
2
là số thuần ảo
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn z - i = 2 v à z 2 là số thuần ảo
Có bao nhiêu số phức z thỏa mãn: |z-i|= 2 và z 2 là số thuần ảo:
A. 3
B. 1
C. 4
D. 2
Có bao nhiêu số phức z thỏa mãn
z
+
i
+
1
z
¯
1
và |z|1 A.0. B.2. C.1. D. 4.
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn z + i + 1 = z ¯ = 1 và |z|=1
A.0.
B.2.
C.1.
D. 4.
Có bao nhiêu nghiệm phức z thỏa mãn |z+i| =2 và z 2 là số thuần ảo?
A. 3
B. 1
C. 4
D. 2
Có bao nhiêu nghiệm phức z thỏa mãn z + i = 2 và z 2 là số thuần ảo?
A. 2
B. 4
C. 1
D. 3
Cho số phức z thỏa mãn ( 1 - 3i) z là số thực và 
. Hỏi có bao nhiêu số phức z thỏa mãn
A. 1
B. 2
C. 3
D. 4
Chọn B.
Gọi số phức cần tìm là z = a + bi.
Ta có ( 1 - 3i) z = ( 1 - 3i) ( a + bi)
= a + 3b - 3ai + bi = a + 3b + ( b - 3a) i
+ Do ( 1 - 3i) z là số thực nên b - 3a = 0 hay b = 3a
+ ta có 
⇔|a – 2 + (-b + 5)i| = 1
Hay ( a - 2) 2 + ( 5 - 3a) 2 = 1
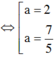(thỏa mãn)
Vậy có hai số phức z thỏa mãn là z = 2 + 6i và z = 7/5 + 21/5i
Đúng 0
Bình luận (0)
Có bao nhiêu số phức z thỏa mãn
(
1
+
i
)
z
+
(
2
-
i
)
z
¯
13
+
2
i
? A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn ( 1 + i ) z + ( 2 - i ) z ¯ = 13 + 2 i ?
A. 4
B. 3
C. 2
D. 1
Đáp án D
Phương pháp:
+) Đặt 
, thay vào phương trình.
+) So sánh hai số phức 
Cách giải: Đặt 
, khi đó ta có:
Đúng 0
Bình luận (0)