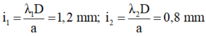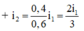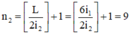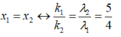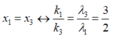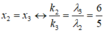Chiếu đồng thời hai ánh sáng đơn sắc có bước sóng l 1 = 0,4 µ m và l 2 = 0,6 µm vào hai khe của thí nghiệm Iâng. Biết khoảng cách giữa hai khe a = 1 mm, khoảng cách từ hai khe tới màn D = 3m, bề rộng vùng giao thoa quan sát được trên màn L = 1,3 cm. Số vị trí vân sáng của hai bức xạ trùng nhau trong vùng giao thoa là
A. 3
B. 2
C. 5
D. 4