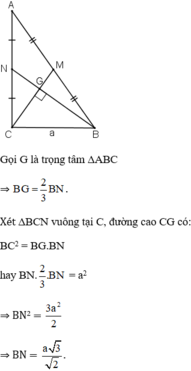
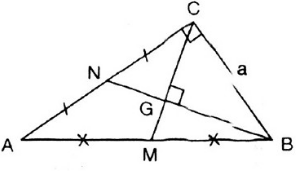
Cho tam giác ABC vuông ở C có đường trung tuyến BN vuông góc với đường trung tuyến CM, cạnh BC = a. Tính độ dài đường trung tuyến BN.

Những câu hỏi liên quan
Cho tam giác ABC vuông ở C có đường trung tuyến BN vuông góc với đường trung tuyến CM, cạnh BC = a. Tính độ dài đường trung tuyến BN.
Cho tam giác ABC vuông ở C có đường trung tuyến BN vuông góc với đường trung tuyến CM, cạnh BC = a. Tính độ dài đường trung tuyến BN ?
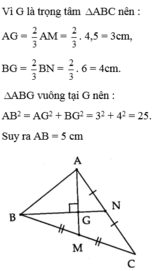
Cho tam giác ABC có hai đường trung tuyến AM, BN vuông góc với nhau, trọng tâm G. Biết AM = 4,5 cm, BN cm. Tính độ dài các cạnh của tam giác ABC.
1.Tam giác ABC vuông tại A có trung tuyến AM vuông góc với trung tuyến BN, cho AB = x. Tính AC, BC theo x?
2. Tam giác ABC vuông tại A có BD là đường phân giác, trung tuyến AM vuông góc BD. Cho BD = \(2\sqrt{3}x\)(x>0). Tính độ dài các cạnh của tam giác ABC?
Cho tam giác ABC, các đường trung tuyến BN và CM vuông góc với nhau.Nếu AB=19, AC=22 thì độ dài cạnh BC là...
Bài 2. Cho tam giác ABC vuông tại A
a) Biết hai trung tuyến BN= 4cm; AM= 3cm. Tính các cạnh của tam giác ABC
b) Biết AB= a, hai đường trung tuyến AM, BN vuông góc với nhau. Tính hai cạnh AC, BC theo a
c) Biết BC= 2a, BM, CN là hai trung tuyến. Tính MB^2 + NC^2 theo a, từ đó tìm GTLN của MB+ NC theo a
a)
Có 2 trung tuyến BN, CM cắt nhau suy ra \(BN\perp AM\)
Gọi G là trọng tâm tam giác ABC, ta có \(BG=\dfrac{2}{3}BN=\dfrac{2}{3}.4=\dfrac{8}{3}\left(cm\right)\)
Trong tam giác ABN vuông tại A, đường cao AG, ta có:
\(AB^2=BG.BN\) (hệ thức lượng)
\(\Rightarrow AB=\sqrt{\dfrac{8}{3}.4}=\dfrac{4\sqrt{6}}{3}\left(cm\right)\)
Tam giác ABN vuông tại A
\(\Rightarrow AN^2=BN^2-AB^2\\ \Rightarrow AN=\sqrt{4^2-\left(\dfrac{4\sqrt{6}}{3}\right)^2}=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
Mà N là trung điểm AC => AC = \(\dfrac{8\sqrt{3}}{3}\left(cm\right)\)
Áp dụng đl pytago vào tam giác ABC:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{4\sqrt{6}}{3}\right)^2+\left(\dfrac{8\sqrt{3}}{3}\right)^2}=4\sqrt{2}\left(cm\right)\)
Thừa dữ kiện AM = 3cm, bạn coi kỹ đề đủ/ đúng hết chưa thì cmt để chút mình coi lại bài giải
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A. Có các đường trung tuyến là AM,BN,CP. Tính độ dài các đường trung tuyến biết rằng BC=a,AC=b,AB=c
cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm.
a)tính độ dài cạnh BC
b)dường trung tuyến AM và đường trung tuyến BN cắt ngay tại G. tính AG.
c) trên tia đối của tia NB ,lấy diểm D sao cho NB = ND chứng minh CD vuông góc AC.
Giúp mik với !!!
a/
\(BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5cm\) (Pitago)
b/
Ta có
\(AM=\dfrac{BC}{2}=\dfrac{5}{2}=2,5cm\) (Trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)
\(AG=\dfrac{2}{3}AM=\dfrac{2}{3}.\dfrac{5}{2}=\dfrac{5}{3}cm\) (trong tg 3 đường trung tuyến đồng quy tại 1 điểm và điểm đó cách đỉnh 1 khoảng bằng 2/3 độ dài đường trung tuyến mà trung tuyến đó đi qua)
c/
Xét tg ABN và tg CDN có
AN=CN (gt); BN=DN (gt)
\(\widehat{ANB}=\widehat{CND}\) (Góc đối đỉnh)
=> tg ABN=tg CDN (c.g.c)=> \(\widehat{BAN}=\widehat{DCN}=90^o\Rightarrow CD\perp AC\)
Đúng 1
Bình luận (0)
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.Câu 2: Cho hình thang cân ABCD, đáy lớn CD10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.Câu 4: Cho tam giác ABC vuông tại A, ABAC; gọi I là giao điểm các đường phân giác, M là...
Đọc tiếp
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.
Câu 2: Cho hình thang cân ABCD, đáy lớn CD=10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.
Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.
Câu 4: Cho tam giác ABC vuông tại A, AB<AC; gọi I là giao điểm các đường phân giác, M là trung điểm BC . Cho biết góc BIM bằng 90°. Tính BC:AC:AB.
Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
Đúng 1
Bình luận (0)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
Đúng 0
Bình luận (0)