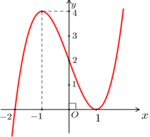
Cho hàm số y = x 3 - 3 x + 2 có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x + 2 - 2 m = 0 có ba nghiệm thực phân biệt.
A. 0<m<4
B. 0<m<2
C. 0 ≤ m ≤ 4
D. 0 ≤ m ≤ 2
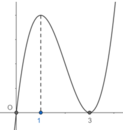
Cho hàm số y=f(x) có đồ thị như hình vẽ bên dưới: Tìm tất cả các giá trị của tham số m để đồ thị hàm số h ( x ) = f 2 ( x ) + f ( x ) + m có đúng 3 điểm cực trị.
A. m ≤ 1
B. m > 1 4
C.m<1
D. m ≥ 1 4
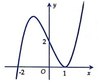
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > − 1
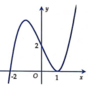
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > 1
Đáp án B.
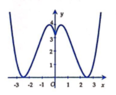
Hàm số y = f x + m là một hàm số chẵn nên đồ thị đối xứng qua trục Oy. Mặt khác y = f x + m = f x + m ∀ x ≥ 0 . Ta có phép biến đổi từ đồ thị hàm số y = f x thành đồ thị hàm số y = f x + m :
* Nếu m > 0:
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang trái m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
* Nếu m=0 :
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang phải m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
Quan sát ta thấy đồ thị hàm số y = f x có 2 điểm cực trị.
Để đồ thị hàm số y = x + m có 5 điểm cực trị thì nhánh bên phải Oy của đồ thị hàm số y = x + m phải có 2 điểm cực trị => Điểm cực trị của đồ thị hàm số y = f x phải được tịnh tiến sang phải O y ⇒ m < − 1 .
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x ) + m có 3 điểm cực trị?
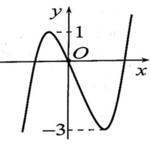
A. 1 ≤ m ≤ 3
B. m = -1 hoặc m = 3
C. m ≤ -1 hoặc m ≥ 3
D. m ≤ -3 hoặc m ≥ 1
Cho hàm số y = f ( x ) có đồ thị như hình vẽ bên dưới. Tìm tất cả các giá trị thực của tham số m để hàm số g x = f x + m có 5 điểm cực trị
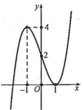
A. m < -1
B. m > -1
C. m > 1
D. m < 1
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x - 1 ) - m - 1 có 3 điểm cực trị?
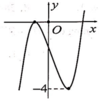
A. -1<m<5
B. - 1 ≤ m ≤ 5
C. m ≥ - 1 hoặc m ≤ - 5
D. m>-1 hoặc m<-5
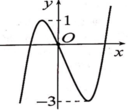
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f x + m có 3 điểm cực trị?
A. 1 ≤ m ≤ 3
B. m = -1 hoặc m = 3
C. m ≤ - 1 h o ặ c m ≥ 3
D. m ≤ - 3 hoặc m ≥ 1
Chọn đáp án C
Dựa vào đồ thị ta thấy đồ thị hàm số y = f(x) có 2 điểm cực trị.
Để đồ thị hàm số y = f x + m có 3 điểm cực trị thì đường thẳng y= -m cắt đồ thị y = f(x) tại 1 điểm duy nhất.
(Không tính điểm cực trị của đồ thị hàm số y = f(x))
Dựa vào đồ thị:
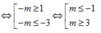
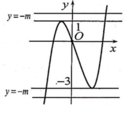
Cho hàm số y = − x 3 − 3 x 2 + 2 có đồ thị hàm số như hình vẽ bên.
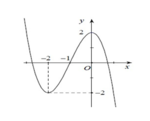
Tìm tập hợp S tất cả các giá trị của tham số thực m sao cho phương trình − x 3 − 3 x 2 + 2 = m có 3 nghiệm phân biệt.
A. S = ∅
B. S = − 2 ; 2
C. S = − 2 ; 1
D. S = − 2 ; 2
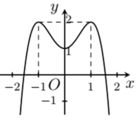
Cho hàm số y =f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + 1 = m có bốn nghiệm thực phân biệt?
![]()
![]()
![]()
![]()
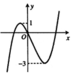
Cho hàm số bậc ba y = f(x) có đồ thị như hình bên. Tất cả các giá trị của tham số m để hàm số y = |f(x)+m| có 3 điểm cực trị là:
A. m ≤ -1 hoặc m ≥ 3
B. m ≤ -3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3