Trong không gian Oxyz, tìm tất cả các giá trị của tham số m để x 2 + y 2 + z 2 + 2 x - 4 y + 4 z + m = 0 là phương trình mặt cầu.
A. m > 9
B. m ≤ 9
C. m < 9
D. m ≥ 9
Trong không gian Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + ( y + 1 ) 2 + ( z + 2 ) 2 = 4 và mặt phẳng (P): 4x-3y-m=0. Tìm tất cả các giá trị thực của tham số m để mặt phẳng (P) và mặt cầu (S) có đúng 1 điểm chung
A. m=1
B. m=-1 hoặc m=-21
C. m=1 hoặc m=21
D. m=-9 hoặc m=31
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x + 3 ) 2 + y 2 + ( z - 2 ) 2 = m 2 + 4 . Tìm tất cả các giá trị thực của tham số m để mặt cầu (S) tiếp xúc với mặt phẳng (Oyz).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d 1 : x + 1 2 = 1 - y - m = 2 - z - 3 và d 2 : x - 3 1 = y 1 = z - 1 1 . Tìm tất cả các giá trị thực của m để d 1 ⊥ d 2 được:
A. -1
B. 1
C. -5
D. 5
Trong không gian tọa độ Oxyz, tìm tất cả các giá trị của tham số m đường thẳng d : x - 2 - 2 = y + 2 1 = z - 1 1 song song với mặt phẳng P : 2 x + 1 - 2 m y + m 2 z + 1 = 0 .
A. m ∈ - 1 ; 3
B. m = 3
C. m = -1
D. Không có giá trị nào của m.
Chọn đáp án B

MEMORIZE |
Vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. |

Trong không gian với hệ toạ độ Oxyz, cho đường thẳng Δ : x - 1 1 = y + 2 2 = z + 1 - 1 và mặt phẳng ( α ) :mx+10y-5z+1=0. Tìm tất cả các giá trị của tham số m để Δ ⊥ ( α ) .
A. m=-25.
B. m=5.
C. m=25.
D. m=-5.
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình x = 6 + t y = - 2 - 5 t z = - 1 + t . Xét đường thẳng ∆ : x - a 5 = y - 1 - 12 = z + 5 - 1 , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và ∆ cắt nhau.
A. a = 0
B. a = 4
C. a = 8
D. a = 1 2
Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8
Trong không gian Oxyz, cho mặt cầu: (S): x - 2 2 + y + 1 2 + z + 2 2 = 4 và mặt phẳng (P): 4x-3y -m =0 Tìm tất cả các giá trị thực của tham số m để mặt phẳng (P) và mặt cầu (S) có đúng 1 điểm chung.
A. m=1
B. m=-1 hoặc m=-21
C. m=1 hoặc m=21
D. m=-9 hoặc m=31
Đáp án C
Mặt cầu (S) tâm I(2;-1;-2) và bán kính R =2. Để mặt phẳng (P) và mặt cầu (S) có đúng 1 điểm chung thì

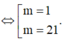
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): mx + 2y - z + 1 = 0 (m là tam số). Mặt phẳng (P) cắt mặt cầu (S): x - 2 2 + y - 1 2 + z 2 = 9 theo một đường tròn có bán kính bằng 2. Tìm tất cả các giá trị thực của tham số m.
A. m = ± 1
B. m = ± 2 + 5
C. m = 6 ± 2 5
D. m = ± 4
Đáp án C.
Mặt cầu (S) có tâm I(2;1;0) bán kính R = 3. Ta có d I ; P = 3 2 - 2 2 = 5
Do đó 2 m + 3 m 2 + 5 = 5 ⇔ 2 m + 3 2 = 5 m 2 + 25 ⇔ m = 6 ± 2 5 .
Trong không gian Oxyz, cho mặt cầu: S : x − 2 2 + y + 1 2 + z + 2 2 = 4 và mặt phẳng P : 4 − 3 y − = 0. Tìm tất cả các giá trị thực của tham số m để mặt phẳng (P)và mặt cầu (S) có đúng 1 điểm chung.
A. m = 1
B. m = - 1 hoặc m = − 21
C. m = 1 hoặc m = 21
D. m = − 9 hoặc m = 31
Đáp án C
Mặt cầu (S)tâm I 2 ; − 1 ; − 2 và bán kính R = 2. . Để mặt phẳng (P)và mặt cầu (S)có đúng 1 điểm chung thì d I ; P = R ⇔ 4.2 − 3 − 1 − m 4 2 + 3 2 = 2 ⇔ m = 1 m = 21 .