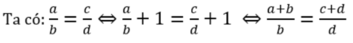Từ tỉ lệ thức a b = c d Hãy suy ra các tỉ lệ thức sau: a a + b = c c + d ( v ớ i a + b ≠ 0 , c + d ≠ 0 )

Những câu hỏi liên quan
từ tỉ lệ thức a/b = c/d hãy suy ra các tỉ lệ thức sau:
a) a+b/b = c+d/d
b) a/a+b = c/c+d
a/b = c/d
=> a/b + 1 = c/d + 1
=> a/b + b/b = c/d + d/d
=> a+b/b = c+d/d
Đúng 0
Bình luận (0)
a/b=c/d =k
suy ra a=b.k ; c=d.k
a+b/b=b.k+b.1=b(k+1)=k+1
c+d/d=d.k+d.1=d.(k+1)=k+1
suy ra a+b/b = c+d/d
phần b tương tự nha !!!
Đúng 0
Bình luận (0)
từ tỉ lệ thức a/b=c/d hãy suy ra các tỉ lệ thức sau:
a: a^2-b^2/c^2-d^2=a.b
Cho tỉ lệ thức a/b=c/d hãy suy ra các tỉ lệ thức sau: (a-b)/b=(c-d)/d
\(\dfrac{a}{b}=\dfrac{c}{d}\)
=>\(\dfrac{a}{b}-1=\dfrac{c}{d}-1\)
=>\(\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
Đúng 0
Bình luận (0)
từ tỉ lệ thức a/b = c/d hãy suy ra các tỉ lệ thức sau
a)a+b/a = c+d/c b) a-b/a = c-d/c
a) a/b = c/d suy ra a/c = b/d = a+b/c+d
từ a/c = a+b/c+d suy ra a+b/a = c+d/c
b) a/b = c/d suy ra a/c = b/d = a-b/c-d
từ a/c = a-b/c-d suy ra a-b/a = c-d/c
Đúng 1
Bình luận (0)
a)Đặt a/b=c/d=k
=>a=bk
c=dk
Vế trái : a+b/a=bk+b/bk
=b(k+1)/bk=k+1/k
Vế phải: c+d/c=ck+c/ck
=c(k+1)/ck=k+1/k
Vì vế trái = vế phải
nên a+b/a=c+d/c
b) Đặt a/b=cd=k
=>a=bk
c=dk
Vế trái : a-b/a=bk-b/bk
=b(k-1)/bk=k-1/k
Vế phải: c-d/c=ck-c/ck
=c(k-1)/ck=k-1/k
Vì vế trái = vế phải
nên a-b/a=c-d/c
Đúng 0
Bình luận (0)
tôi có một công thức chưa ai phát hiện ra đó là nếu a/b=c/d=>hai số này bằng tích của nó là a*c/b*d
Đúng 0
Bình luận (0)
từ tỉ lệ thức a/b=c/d hãy suy ra các tỉ lệ thức sau
a) a+b/b=c+d/d
hãy viết phép tính cho mình nhé
\(a.\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\Rightarrow\frac{a+b}{b}=\frac{c+d}{d}.\)
Đúng 0
Bình luận (0)
từ tỉ lệ thức a/b-c/d hãy suy ra tỉ lệ thức a/c=b/d
Đề bài : từ tỉ lệ thức a/b =c/d hãy suy ra các tỉ lệ thức sau:
a, a+b/b=c+d/d
b, a/a+b =c/c+d (với a+b khác 0, c+d khác 0)
Từ tỉ lệ thức a b = c d . Hãy suy ra các tỉ lệ thức sau: a + b b = c + d d
Từ tỉ lệ thức a/b=c/d(a,b,c,d khác 0; a khác +-b; c khác +-d) hãy suy ra tỉ lệ thức sau
a/a+b=c/c+d
ta có :\(\frac{a}{b}=\frac{c}{d}->\frac{a}{c}=\frac{b}{d}\)
áp dụng t/c của dãy t/s = nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}->\frac{a}{c}=\frac{a+c}{b+d}=\frac{a}{a+b}=\frac{c}{c+d}\left(dpcm\right)\)
Đúng 0
Bình luận (0)