Giải các bất phương trình lôgarit sau: lnx + 2 lnx - 1 < 0

Những câu hỏi liên quan
Giải các phương trình sau:
a) e 2 + ln x = x + 3;
b) e 4 - ln x = x;
c) (5 − x).log(x − 3) = 0
a) Với điều kiện x > 0, ta có phương trình
e 2 . e ln x = x + 3
⇔ e 2 .x = x + 3
⇔x( e 2 − 1) = 3
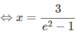
(thỏa mãn điều kiện)
b) Tương tự câu a), x = e 2
c) Với điều kiện x > 3 ta có:
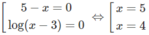
Đúng 0
Bình luận (0)
Giải các phương trình sau: ln(4x + 2) - ln(x - 1) = lnx
Với điều kiện x > 1 ta có phương trình:
ln(4x + 2) = ln[x(x − 1)]
⇔ 4x + 2 = x 2 – x ⇔ x 2 – 5x – 2 = 0
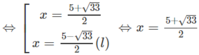
Đúng 0
Bình luận (0)
Giải các phương trình sau: e 2 + lnx = x + 3
Với điều kiện x > 0, ta có phương trình
e 2 . e lnx = x + 3
⇔ e 2 .x = x + 3
⇔x( e 2 − 1) = 3
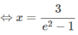
(thỏa mãn điều kiện)
Đúng 0
Bình luận (0)
Giải các phương trình sau: e 4 - lnx = x + 3
Giải các bất phương trình lôgarit sau: log x 2 - x - 2 < 2 log 3 - x
Bất phương trình đã cho tương đương với hệ:
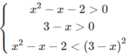
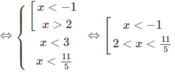
Vậy tập nghiệm là (− ∞ ; −1) ∪ (2; 11/5)
Đúng 0
Bình luận (0)
Giải các bất phương trình lôgarit sau:
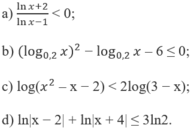
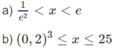
c) Bất phương trình đã cho tương đương với hệ:
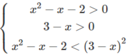
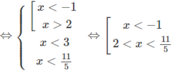
Vậy tập nghiệm là (− ∞ ; −1) ∪ (2; 11/5)
d) ln|(x − 2)(x + 4)| ≤ ln8
⇔| x 2 + 2x − 8| ≤ 8
⇔ −8 ≤ x 2 + 2x – 8 ≤ 8
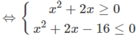
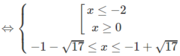
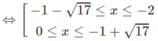
Vậy tập nghiệm là
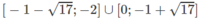
Đúng 0
Bình luận (0)
Giải các bất phương trình lôgarit sau: ln|x - 2| + ln|x + 4| ≤ 3ln2
ln|(x − 2)(x + 4)| ≤ ln8
⇔| x 2 + 2x − 8| ≤ 8
⇔ −8 ≤ x 2 + 2x – 8 ≤ 8
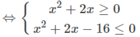
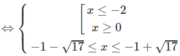
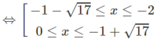
Vậy tập nghiệm là
![]()
Đúng 0
Bình luận (0)
Giải các bất phương trình lôgarit sau: log 0 , 2 x 2 - log 0 , 2 x - 6 ≤ 0
Phương trình
ln
x
-
1
2
.
ln
x
+
1
2
.
ln
x
+
1
4
.
ln
x
+
1...
Đọc tiếp
Phương trình ln x - 1 2 . ln x + 1 2 . ln x + 1 4 . ln x + 1 8 có bao nhiêu nghiệm?
A. 3
B. 4
C. 1
D. 2
Điều kiện:
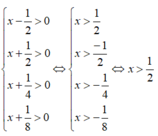
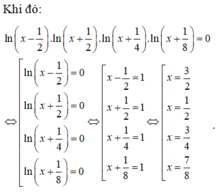
So với điều kiện, ta được tập nghiệm của phương trình là S = 3 2 ; 3 4 ; 7 8
Vậy phương trình đã cho có 3 nghiệm
Đáp án A
Đúng 0
Bình luận (0)


