Trong không gian, cho tam giác ABC vuông tại A, AB=a, A C B ⏜ = 60 0 . Quay tam giác đó một vòng xung quanh BC, ta được một hình tròn xoay. Tính diện tích xung quanh S x q của hình tròn xoay đó.
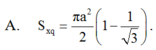
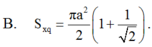
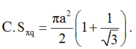
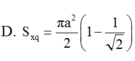
Trong không gian cho tam giác ABC vuông tại B, B C = a , A C B ^ = 60 ° . Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AB.
A. πa 2
B. 2 πa 2
C. πa 2 2
D. 4 πa 2
Đáp án B.


Khi quay tam giác ABC quanh cạnh AB, ta được khối nón có đỉnh A, đường sinh

Trong không gian cho tam giác ABC vuông tại B, B C = a , A C B ^ = 60 ° . Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AB.
A. πa 2
B. 2 πa 2
C. πa 2 2
D. 4 πa 2
Đáp án B.
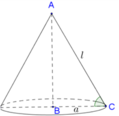
Khi quay tam giác ABC quanh cạnh AB, ta được khối nón có đỉnh A, đường sinh
Trong không gian Oxyz, cho tam giác ABC vuông tại C, A B C ^ = 60 ° , A B = 3 2 . Đường thẳng AB có phương trình x − 3 1 = y − 4 1 = z + 8 − 4 , đường thẳng AC nằm trên mặt phẳng α : x + z − 1 = 0. Biết B là điểm có hoành độ dương, gọi a ; b ; c là tọa độ của điểm C, giá trị của a+b+c bằng
A. 3
B. 2
C. 4
D. 7
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC vuông tại C có A B C ^ = 60 ° ; A B = 3 2 . Đường thẳng AB có phương trình x - 3 1 = y - 4 1 = x + 8 - 4 , đường thẳng AC nằm trên mặt phẳng α : x + z - 1 = 0 . Biết điểm B là điểm có hoành độ dương, gọi (a,b,c) là tọa độ của điểm C. Giá trị a + b + c bằng
A. 2
B. 3
C. 4
D. 7
Tọa độ điểm là nghiệm của hệ 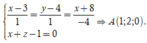
Gọi ![]() Vì
Vì ![]()
Từ ![]()
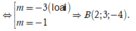
Ta có 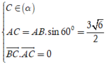
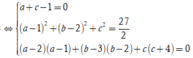
Giải hệ trên ta được ![]() Vậy a + b + c = 4.
Vậy a + b + c = 4.
Chọn C.
Trong không gian, cho tam giác ABC vuông tại A, AB=a, ABC=60 ° . Quay tam giác đó một vòng xung quanh BC, ta được một hình tròn xoay. Diện tích xung quanh của hình tròn xoay đó bằng
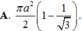
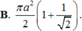
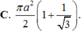
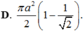
Trong không gian, cho tam giác ABC vuông tại A, A B = a , A B C = 60 ° . Quay tam giác đó một vòng xung quanh BC, ta được một hình tròn xoay. Diện tích xung quanh của hình tròn xoay đó bằng
A. πa 2 2 1 - 1 3
B. πa 2 2 1 + 1 2
C. πa 2 2 1 + 1 3
D. πa 2 2 1 - 1 2
Trong không gian, cho tam giác ABC vuông tại A, AB=a, góc ACB bằng 60 ° . Quay tam giác đó một vòng xung quanh BC, ta được một hình tròn xoay. Tính diện tích xung quanh của hình tròn xoay đó
A. πa 2 2 ( 1 - 1 3 )
B. πa 2 2 ( 1 + 1 2 )
C. πa 2 2 ( 1 + 1 3 )
D. πa 2 2 ( 1 - 1 2 )
Trong không gian, cho tam giác ABC vuông tại A, AB = a và AC = a 3 . Khi quay tam giác ABC xung quanh AB, ta được một khối nón có độ dài đường sinh là:
A. l = 2a B. l = a 2
C. l = a 3 D. l = a
Chọn A.
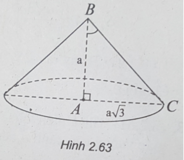
(h.2.63) Độ dài đường sinh l bằng độ dài cạnh BC của tam giác vuông ABC.
Theo định lý Py-ta-go, ta có:
BC 2 = AB 2 + AC 2 = a 2 + 3 a 2 = 4 a 2
⇒ BC = 2a.
Vậy độ dài đường sinh của hình nón là l = 2a.
Trong không gian cho tam giác ABC vuông tại A, A B = a , A C = a . Tính độ dài đường sinh l của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB.
A. l = a
B. l = a 5
C. l = a 3
D. l = 2 a
Cho tam giác ABC vuông tại A, trên nửa bờ mặt phẳng AB không chứa điểm C đựng tam giác DAB vuông cân tại D. Trên nửa bờ mặt phẳng AC không chứa điểm B đựng tam giác EAC vuông cân tại E, lấy M là trung điểm của cạnh BC. DM cắt AB tại F, ME cắt AC tại K. Chứng minh rằng:
a.Ba điểm D,A,E thẳng hàng.
b. DM vuông góc AB; EM vuông góc AC.
c. Tam giác DME vuông cân .
d. KF song song BC; KF=\(\frac{BC}{2}\).
e. Cho AB = a, góc ABC=600. Tính diện tích hình BDCE ?