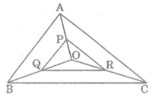
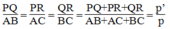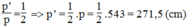cho tam giác ABC. O nằm trong tam giác ABC.M,N,P lần lượt là trung điểm của OA,OB,OC.Hỏi tam giác MNP=mấy lần tam giác ABC

Những câu hỏi liên quan
Cho tam giác ABC và điểm O nằm trong tam giác. Gọi M, N, P lần lượt là trung điểm của OA, OB, OC. Biết chu vi tam giác ABC là 5,5m. Tính chu vi tam giác MNP.
Xét ΔOAB có
M,N lần lượt là trung điểm của OA,OB
=>MN là đường trung bình của ΔOAB
=>\(MN=\dfrac{1}{2}AB\)
Xét ΔOAC có
M,P lần lượt là trung điểm của OA,OC
=>MP là đường trung bình của ΔOAC
=>\(MP=\dfrac{1}{2}AC\)
Xét ΔOBC có
N,P lần lượt là trung điểm của OB,OC
=>NP là đường trung bình của ΔOBC
=>\(NP=\dfrac{1}{2}BC\)
Chu vi tam giác MNP là:
MN+NP+MP
\(=\dfrac{1}{2}\left(AB+CA+BC\right)\)
\(=\dfrac{1}{2}\cdot5,5=2,75\left(m\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC và điểm O nằm trong tam giác. Gọi M, N, P lần lượt là trung điểm của OA, OB, OC. Biết chu vi tam giác ABC bằng 10cm. Tính chu vi tam giác MNP. Chu vi tam giác MNP: cm
Xét tam giác PAC,ta có:
{MP=MAOP=OC
=>MP = 1/2 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 543/2 cm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho điểm O nằm trong tam giác ABC. M,N,P lần lượt là trung điểm của OA,OB,OC. Tính tỉ số diện tích tam giác MNP và tam giác ABC
Xét tam giác PAC,ta có:
{MP=MAOP=OC{MP=MAOP=OC
=>MP = 1212 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 54325432 cm
LÀM LIỀU !!
Nối M với C ; B với P ; N với A
Xét tam giác OMC có : MP là đường trung tuyến ứng với cạnh OC
=> S MOP = S MCP = 1/2. S OMC ( t/c đường trung tuyến trong tam giác )
Xét tam giác AOC có : CM là đường trung tuyến ứng với cạnh OA
=> S OCM = S ACM = 1/2. S OAC ( t/c đường trung tuyến của tam giác )
=> S OMP = 1/4.S OAC
Tương tự CM được S ONP = 1/4 S OBC ; S OMN = 1/4. S OAB
=> S OMP + S OMN + S ONP = 1/4. S OAC + 1/4. S OAB + 1/4 . S OMN
=> S MNP = 1/4. S ABC
=> S MNP / S ABC = 1/4
Cho điểm O nằm trong tam giác ABC . Gọi M,N,P lần lượt là trung điểm của OA,OB,OC. Khi đó tỉ ố diện tích của tam giác MNP và tam giác ABC bằng
Cho tam giác ABC và điểm O nằm trong tam giác. Gọi M, N, P lần lượt là trung điểm của OA, OB, OC. Biết chu vi tam giác ABC là 6m. Tính chu vi tam giác MNP.
Xét tam giác PAC,ta có:
{MP=MAOP=OC
=>MP = 1/2 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 543/2 cm
Cho tam giác ABC và điểm O nằm trong tam giác. Gọi M, N, P lần lượt là trung điểm của OA, OB, OC. Biết chu vi tam giác ABC là 3m. Tính chu vi t
Cho tam giác ABC và điểm O nằm bên trong tam giác đó .M;N;P lần lượt là trung điểm của BC;CA;AB.Trên các tia OM;ON;OP lấy các điểm A';B';C' sao cho M;N;P lần lượt là trung điểm của OA' ;OB';OC'. CM:tam giác ABC=tam giác A'B'C'
PM là đường trung bình của \(\Delta ABC\) nên \(PM=\frac{1}{2}AC\)
Mà PM cũng là ĐTB của \(\Delta OA'C'\) nên \(PM=\frac{1}{2}A'C'\)
Suy ra: \(AC=A'C'\)
Tương tự, ta có: \(PN=\frac{1}{2}BC,PN=\frac{1}{2}B'C'\Rightarrow BC=B'C'\)
\(MN=\frac{1}{2}AB,MN=\frac{1}{2}A'B'\Rightarrow AB=A'B'\)
Vậy \(\Delta ABC=\Delta A'B'C'\left(c.c.c\right)\)
Chúc bạn học tốt.
Đúng 0
Bình luận (0)
Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.
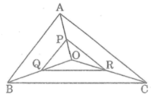
* Trong △ AOB ta có:
P trung điểm của OA (gt)
Q trung điếm của OB (gt)
Suy ra PQ là đường trung bình của △ AOB
Suy ra: PQ = 1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: 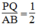 (1)
(1)
* Trong △ OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra PR là đường trung bình của tam giác OAC.
Suy ra: PR =1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: 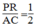 (2)
(2)
* Trong △ OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra QR là đường trung bình của tam giác OBC
Suy ra: QR = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: 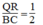 (3)
(3)
Từ (1), (2) và (3) suy ra: 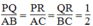
Vậy △ PQR đồng dạng △ ABC (c.c.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543 cm.