Cho hàm số f x = sin x + x - 1 . Xét hai khẳng định sau
(1)Hàm số trên có đạo hàm tại x=1
(2)Hàm số liên tục tại x=1
Trong hai khẳng định trên
A. Chỉ có (1) đúng
B.Chỉ có (2) đúng
C. Cả hai đều đúng
D. Cả hai đều sai
Cho hàm số f(x)=sinx+|x-1| Xét hai khẳng định sau
(1)Hàm số trên có đạo hàm tại ![]()
(2)Hàm số liên tục tại ![]() Trong hai khẳng định trên
Trong hai khẳng định trên
A. Chỉ có (1) đúng
B.Chỉ có (2) đúng
C.Cả hai đều đúng
D. Cả hai đều sai.
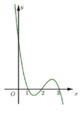
Cho hàm số f(x) xác định trên R và hàm số y = f’(x) có đồ thị như hình bên dưới:
Xét các khẳng định sau:
(I) Hàm số y = f(x) có ba cực trị.
(II) Phương trình f(x) = m + 2018 có nhiều nhất ba nghiệm.
(III) Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
Số khẳng định đúng là:
A. 1
B. 2
C. 0
D. 3
Đáp án B
Phương pháp: Từ đồ thị hàm số y = f’(x) lập BBT của đồ thị hàm số y = f(x) và kết luận.
Cách giải: Ta có 
BBT:
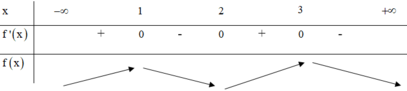
Từ BBT ta thấy (I) đúng, (II) sai.
Với ![]() => Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=> Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=>(III) đúng.
Vậy có hai khẳng định đúng
Cho hàm số y = f(x) xác định trên
ℝ
và có đồ thị hàm số y = f '(x) như hình vẽ bên.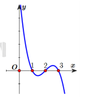 Xét các khẳng định sau:
Xét các khẳng định sau:
(I) Hàm số y = f(x) có ba cực trị.
(II) Phương trình f(x) = m + 2018 có nhiều nhất ba nghiệm.
(III) Hàm số y = f(x + 1) nghịch biến trên khoảng (0;1) .
Số khẳng định đúng là:
A. 1
B. 3
C. 2
D. 0
Đáp án C
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 > 0
ii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực đại tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 < 0
iii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và f ' ' x 0 = 0 thì hàm số không đạt cực trị tại x = x 0
Số khẳng định đúng trong các khẳng định trên là
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau

Gọi g ( x ) = 2 f ( 1 - x ) + 1 4 x 4 - x 3 + x 2 - 5 . Khẳng định nào sau đây đúng?
A. Hàm số g(x) đồng biến trên khoảng - ∞ ; - 2
B. Hàm số g(x) đồng biến trên khoảng (-1;0)
C. Hàm số g(x) đồng biến trên khoảng (0;1)
D. Hàm số g(x) đồng biến trên khoảng 1 ; + ∞
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau

Xét hàm số
g ( x ) = f x - 1 2 - x 3 3 + 3 2 x 2 - 2 x + 3 . Khẳng định nào sau đây sai?
A. Hàm số g(x) nghịch biến trong khoảng ( - 1 ; 0 )
B. Hàm số g(x) đồng biến trên khoảng 0 ; 2
C. Hàm số g(x) nghịch biến trong khoảng - 4 ; - 1
D. Hàm số g(x) đồng biến trên khoảng 2 ; 3
Cho hàm số y= f( x) liên tục và xác định trên R. Biết f( x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ. Xét trên ![]() , khẳng định nào sau đây đúng?
, khẳng định nào sau đây đúng?
A. Hàm số y= f( x) đồng biến trên khoảng ![]() .
.
B. Hàm số y= f( x) nghịch biến trên khoảng ![]() .
.
C. Hàm số y= f(x) nghịch biến trên khoảng - π ; - π 2 và π 2 ; π .
D. Hàm số y= f( x) đồng biến trên khoảng ![]() .
.
Chọn D
Trong khoảng ![]() đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
Xét các khẳng định sau
i) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại α ∈ - 1 ; 1 thỏa mãn f ( x ) ≥ f ( α ) ∀ x ∈ - 1 ; 1 .
ii) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại β ∈ - 1 ; 1 thỏa mãn f ( x ) ≤ f ( β ) ∀ x ∈ - 1 ; 1 .
iii) Nếu hàm số y = f(x) xác định trên [-1;1] thỏa mãn f(-1).f(1)<0 thì tồn tại γ ∈ - 1 ; 1 thỏa mãn f ( γ ) = 0
Số khẳng định đúng là
A. 3.
B. 2.
C. 1.
D. 0.
Cho hàm số f(x) liên tục trên ℝ hàm số y = f '(x) có đồ thị như hình vẽ. Xét hàm số h x = 2 f 3 x + 1 - 9 x 2 - 6 x + 4 . Hãy chọn khẳng định đúng:

A. Hàm số h(x) nghịch biến trên ℝ
B. Hàm số h(x) nghịch biến trên - 1 ; 1 3
C. Hàm số h(x) đồng biến trên - 1 ; 1 3
D. Hàm số h(x) đồng biến trên ℝ