Các đường cong ở hình bên là đồ thị của hàm số y = a x + b c x + d với a,b,c,d là các số thực. Mệnh đề nào sau đây đúng?
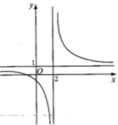
A. y ' < 0 , ∀ x ≠ 2
B. y ' < 0 , ∀ x ≠ 1
C. y ' > 0 , ∀ x ≠ 2
D. y ' > 0 , ∀ x ≠ 1
Những câu hỏi liên quan
Đường cong ở hình vẽ bên dưới là đồ thị của hàm số
y
a
x
4
+
b
x
2
+
c
với a, b, c là các số thực. A. Phương trình y 0 vô nghiệm trên tập số thực B. Phương trình y 0 có ba nghiệm thực phân biệt C.Phương trình y 0 có hai nghiệm thực phân biệt D. Phương trình y 0 có đúng một nghiệm thực
Đọc tiếp
Đường cong ở hình vẽ bên dưới là đồ thị của hàm số y = a x 4 + b x 2 + c với a, b, c là các số thực.
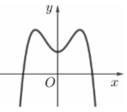
A. Phương trình y ' = 0 vô nghiệm trên tập số thực
B. Phương trình y ' = 0 có ba nghiệm thực phân biệt
C.Phương trình y ' = 0 có hai nghiệm thực phân biệt
D. Phương trình y ' = 0 có đúng một nghiệm thực
Đáp án B
Phương pháp:
Quan sát đồ thị, đếm số cực trị của đồ thị hàm số và suy ra số nghiệm của phương trình y ' = 0 .
Cách giải:
Đồ thị hàm số có 3 điểm cực trị hay hàm số có 3 điểm cực trị. Do đó phương trình y ' = 0 có ba nghiệm thực phân biệt.
Đúng 0
Bình luận (0)
Đường cong ở hình vẽ bên dưới là đồ thị của hàm số y ax 4 + bx 2 + c với a, b, c là các số thực A. Phương trình y 0 vô nghiệm trên tập số thực B. Phương trình y 0 có ba nghiệm thực phân biệt C.Phương trình y 0 có hai nghiệm thực phân biệt D. Phương trình y 0 có đúng một nghiệm thực
Đọc tiếp
Đường cong ở hình vẽ bên dưới là đồ thị của hàm số y = ax 4 + bx 2 + c với a, b, c là các số thực
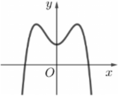
A. Phương trình y ' = 0 vô nghiệm trên tập số thực
B. Phương trình y ' = 0 có ba nghiệm thực phân biệt
C.Phương trình y ' = 0 có hai nghiệm thực phân biệt
D. Phương trình y ' = 0 có đúng một nghiệm thực
Chọn B
Đồ thị hàm số có 3 điểm cực trị hay hàm số có 3 điểm cực trị.
Do đó phương trình y ' = 0 có ba nghiệm thực phân biệt
Đúng 0
Bình luận (0)
Đường cong ở hình bên là đồ thị của hàm số
y
a
x
4
+
b
x
2
+
c
với a,b,c là các số thực. Mệnh đề nào dưới đây đúng? A. Phương trình
y
0
có đúng một nghiệm thực B. Phương trình
y
0
có đúng hai nghiệm t...
Đọc tiếp
Đường cong ở hình bên là đồ thị của hàm số y = a x 4 + b x 2 + c với a,b,c là các số thực. Mệnh đề nào dưới đây đúng?
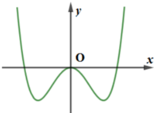
A. Phương trình y ' = 0 có đúng một nghiệm thực
B. Phương trình y ' = 0 có đúng hai nghiệm thực phân biệt
C. Phương trình y ' = 0 vô nghiệm trên tập số thực
D. Phương trình y ' = 0 có đúng ba nghiệm thực phân biệt.
Đáp án D
Phương pháp
Số nghiệm của đạo hàm hàm số bậc bốn trùng phương bằng số cực trị của hàm số.
Cách giải:
Nhận xét: Đồ thị hàm số đã cho có 3 điểm cực trị → Phương trình y ' = 0 có đúng ba nghiệm thực phân biệt.
Đúng 0
Bình luận (0)
Đường cong ở hình bên là đồ thị của hàm số
y
a
x
+
b
c
x
+
d
với a, b, c là các số thực.Mệnh đề nào dưới đây đúng?
Đọc tiếp
Đường cong ở hình bên là đồ thị của hàm số
y
=
a
x
+
b
c
x
+
d
với a, b, c là các số thực.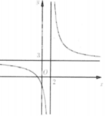
Mệnh đề nào dưới đây đúng?
Đường cong ở hình bên là đồ thị của hàm số
y
a
x
4
+
b
x
2
+
c
với a,b,c là các số thực. Mệnh đề nào dưới đây đúng? A. Phương trình y0 có đúng một nghiệm thực B. Phương trình y0 có đúng hai nghiệm thực phân biệt. C. Phương trình y0 vô nghiệm trên tập số thực. D. Phương trình y0 có đúng ba nghiệm thực phân biệt
Đọc tiếp
Đường cong ở hình bên là đồ thị của hàm số y = a x 4 + b x 2 + c với a,b,c là các số thực. Mệnh đề nào dưới đây đúng?
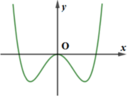
A. Phương trình y'=0 có đúng một nghiệm thực
B. Phương trình y'=0 có đúng hai nghiệm thực phân biệt.
C. Phương trình y'=0 vô nghiệm trên tập số thực.
D. Phương trình y'=0 có đúng ba nghiệm thực phân biệt
Nhận xét: Đồ thị hàm số đã cho có 3 điểm cực trị ⇒ Phương trình y'=0 có đúng ba nghiệm thực phân biệt.
Chọn đáp án D.
Đúng 0
Bình luận (0)
Đường cong ở hình bên là đồ thị của hàm số
y
a
x
+
b
c
x
+
d
với a, b, c là các số thực. Mệnh đề nào dưới đây đúng? A.
y
0
,
∀
x
≠
2
. B.
y...
Đọc tiếp
Đường cong ở hình bên là đồ thị của hàm số
y = a x + b c x + d với a, b, c là các số thực. Mệnh đề nào dưới đây đúng?
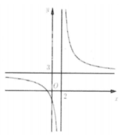
A. y ' > 0 , ∀ x ≠ 2 .
B. y ' > 0 , ∀ x ≠ 3 .
C. y ' < 0 ∀ x ≠ 2 .
D. y ' < 0 , ∀ x ≠ 3
Đáp án C
Dựa vào đổ thị ta thấy hàm số giảm trên từng khoảng xác định nên
Đúng 0
Bình luận (0)
Các đường cong ở hình bên là đồ thị của hàm số
y
a
x
+
b
c
x
+
d
với a,b,c,d là các số thực. Mệnh đề nào sau đây đúng? A. B. C. D.
Đọc tiếp
Các đường cong ở hình bên là đồ thị của hàm số y = a x + b c x + d với a,b,c,d là các số thực. Mệnh đề nào sau đây đúng?
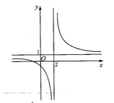
A.
B. 
C. 
D. 
Đường cong ở hình bên là đồ thị của hàm số
y
a
x
+
b
c
x
+
d
với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng? A.
y...
Đọc tiếp
Đường cong ở hình bên là đồ thị của hàm số y = a x + b c x + d với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng?
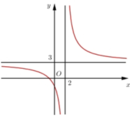
A. y ' < 0 ∀ x ≠ 2
B. y ' < 0 ∀ x ≠ 3
C. y ' > 0 ∀ x ≠ 3
D. y ' > 0 ∀ x ≠ 2
Đáp án A.
Phương pháp: Dựa vào các đường tiệm cận và sự đơn điệu của đồ thị hàm số.
Cách giải: Ta thấy hàm số nghịch biến trên (-∞;2) và (2;+ ∞) => y ' < 0 ∀ x ≠ 2
Đúng 0
Bình luận (0)
Đường cong ở hình vẽ bên là đồ thị của hàm số y=f(x).
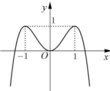
Số nghiệm của phương trình 2f(x)-1=0 là
A. 2.
B. 4.
C. 0.
D. 3.