Tìm các số phức 2z +
z
và 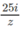 biết rằng z = 3 – 4i
biết rằng z = 3 – 4i
(Đề thi tốt nghiệp THPT năm 2012)
Tìm các số phức 2z + z ¯ và 25 i z biết rằng z = 3 – 4i
(Đề thi tốt nghiệp THPT năm 2012)
2z + z ¯ = 2(3 − 4i) + 3 + 4i = 6 − 8i + 3 + 4i = 9 − 4i
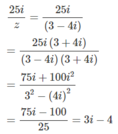
Giải phương trình: z - i 2 + 4 = 0 trên tập số phức.
(Đề thi tốt nghiệp THPT năm 2011)
Giải phương trình: ( z - i ) 2 + 4 = 0 trên tập số phức.
(Đề thi tốt nghiệp THPT năm 2011)
Giải phương trình sau trên tập số phức:
(1 – i)z + (2 – i) = 4 – 5i
(Đề thi tốt nghiệp THPT năm 2011)
(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
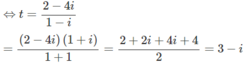
Giải phương trình sau trên tập số phức: (1 – i)z + (2 – i) = 4 – 5i (Đề thi tốt nghiệp THPT năm 2011)
(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
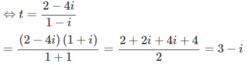
Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z – (3 – 4i)|=2
(Đề thi Đại học năm 2009, khối D)
Đặt z = x + yi. Từ |z – (3 – 4i)| = 2 suy ra:
x - 3 2 + y + 4 2 = 4
Các điểm biểu diễn z nằm trên đường tròn tâm I(3; -4) bán kính 2
Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z – (3 – 4i)|=2
(Đề thi Đại học năm 2009, khối D)
Đặt z = x + yi. Từ |z – (3 – 4i)| = 2 suy ra:
( x - 3 ) 2 + ( y + 4 ) 2 = 4
Các điểm biểu diễn z nằm trên đường tròn tâm I(3; -4) bán kính 2.
Tìm các số phức \(2z+\overline{z}\) và \(\dfrac{25i}{z}\) biết rằng \(z=3-4i\)
Biết các số phức z thỏa mãn |z-3|=|z+4i|. Tìm w m i n biết w = z + 4i -3
A. w m i n = 7 5
B. w m i n = 7 10
C. w m i n = 7 12
D. w m i n = 7