Cho hàm số y = sin x - cos x + 1 sin x + cos x + 2 . Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó giá trị của M+m là

A. 2

B. 4

C. 0

D. 1

Cho hàm số y = sin x - cos x + 1 sin x + cos x + 2 . Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó giá trị của M + m là

A. 2

B. 4

C. 0

D. 1

Cho hàm số y = sinx − cosx + 1 sinx + cosx − 2 . Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó giá trị của M+m là

A. 1

B. 4

C. 2

D. 0

Giả sử M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 - 9 x 2 + 24 x - 68  trên đoạn [ -1;4 ]. Khi đó giá trị m M  bằng

A.  7 17

B.  8 17

C.  9 17

D.  10 17

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = l n ( 2 x 2 + e 2 ) trên [0;e]. Mệnh đề nào sau đây đúng

A. M + m = 5

B. M + m = 4 + ln3

C. M + m = 4 + ln2

D. M + m = 2 + ln3

Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = x = ln(x) trên đoạn 1 2 ; e  lần lượt là

A. 1 và e - 1

B. 1 và e

C.  1 2 + ln 2   và e - 1

D. 1 và  1 2 + ln 2

Gọi M; N lần lượt là giá trị nhỏ nhất, lớn nhất của hàm số  y   =   ln ( x + x 2 + 4 )  trên đoạn [0;5] Khi đó tổng M+N là

A.

B.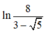 

C. .

D. Kết quả khác

Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = sin   x + 2   cos   x + 1 sin   x + cos   x + 2  là

A.  m = - 1 2 ;   M = 1

B.  m = 1 ;   M = 2

C.  m = - 2 ;   M = 1

D.  m = - ;   M = 2

Giá trị nhỏ nhất m và giá trị lớn nhất M  của hàm số y   =   sin   x   +   2   cos   x   +   1 sin   x   +   cos   x   +   2  là