Cho hình nón tròn xoay có độ dài đường sinh là 2a , góc ở đỉnh của hình nón bằng 60 ° . Thể tích V của khối nón đã cho là
A. V = πa 3 3
B. V = π 3 a 3
C. V = π a 3
D. π 3 a 3 3
Cho hình nón tròn xoay có độ dài đường sinh là 2a, góc ở đỉnh của hình nón bằng 60 ° . Thể tích V của khối nón đã cho là
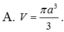
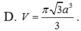
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Chọn C.
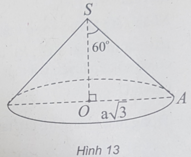
(h.13) Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết, đường tròn đáy có bán kính R = OA = a 3 và ∠ = 60 °
Trong tam giác SOA vuông tại O, ta có: OA = SO.tan60 ° ⇒ SO = a.
Do đó chiều cao của hình nón là h = a.
Vậy thể tích hình nón là: V = π a 3
Cho khối nón tròn xoay có góc ở đỉnh là 60o và đường sinh l = 6cm. Thể tích của khối nón là:
A. 9π 3 (c m 3 )
B. 27π 3 (c m 3 )
C. 27π (c m 3 )
D. 3π 3 (c m 3 )
Hình nón có góc ở đỉnh là 9 0 o và có diện tích xung quanh là π 2 . Độ dài đường cao của hình nón là:
A. 1
B. 2
C. 1/ 2
D. 2
Đáp án A
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
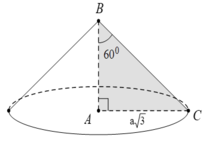
Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a 2 và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh S xq của hình nón và thể tích V của khối nón tương ứng là:
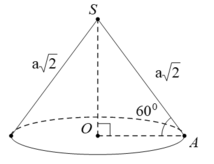
A. S xq = πa 2 ; V = πa 3 6 12
B. S xq = πa 2 2 ; V = πa 3 3 12
C. S xq = πa 2 2 ; V = πa 3 6 4
D. S xq = πa 2 ; V = πa 3 6 4
Đáp án A
Gọi A là một điểm thuộc đường tròn đáy hình nón. Theo giải thiết ta có đường sinh SA = a 2 và góc giữa đường sinh và mặt phẳng đáy là SAO ^ = 60°.
Cho khối nón có độ lớn góc ở đỉnh là π 3 . Một khối cầu ( S 1 ) nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 1 ;..; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , . . . . . , V n - 1 , V n , lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , . . . . . , S n - 1 , S n , và V là thể tích của khối nón. Tính giá trị của biểu thức T = l i m V 1 + V 2 + . . . + V n V .
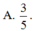
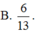
Cho khối nón có độ lớn góc ở đỉnh là π 3 . Một khối cầu ( S 1 ) nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 2 ;…; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , … , V n - 1 , V n lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , … , S n và V là thể tích của khối nón. Tính giá trị của biểu thức T = lim n → + ∞ V 1 + V 2 + . . . + V n V
A. 3 5
B. 6 13
C. 7 9
D. 1 2
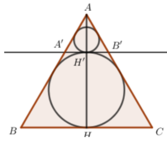
Chọn đáp án B
Thiết diện qua trục của hình nón là một tam giác đều cạnh l.
Do đó bán kính đường tròn nội tiếp tam giác cũng chính là bán kính mặt cầu nội tiếp chóp là
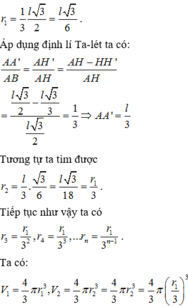
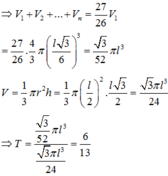
Cho hình nón có độ dài đường sinh l = 2a, góc ở đỉnh của hình nón 2 β = 60 ° . Tính thể tích V của khối nón đã cho
A. V = π a 3
B. V = π a 3 2
C. V = π a 3 3 3
D. V = π a 3 3
Đáp án C
Ta có R = l . sin 30 ° = 2 a . 1 2 = a h = l . cos 30 ° = 2 a . 3 2 = a 3 → V = 1 3 πR 2 . h = 1 3 πa 2 . a 3 = 3 3 πa 3 .
