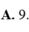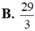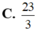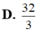Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f x = sinxcosx , đường thẳng y = 0 , x = 0 và x = π 2
A. 1
B. 1 2
C. π 2
D. 1 4
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f ( x ) = sinx cosx , đường thẳng y = 0 , x = 0 và x = π 2 .
A. 1 2
B. 1
C. 1 4
D. π 2
Tính diện tích hình phẳng giới hạn bởi : Đồ thị hàm số y = e x +1 , trục hoành , đường thẳng x = 0 và đường thẳng x = 1
A.e
B. 2+e
C.e-1
D.2e+1
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
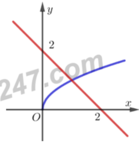
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Cho hàm số y = f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b. Diện tích hình phẳng D được tính bởi công thức.
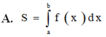
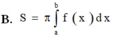
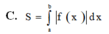
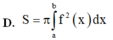
Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số y = sin x , y = cos x và hai đường thẳng x = 0 , x = π 2 ?
A. S = 2 2
B. S = 2 1 − 2
C. S = 2 2 − 1
D. S = 2 2 − 1
Đáp án C
∫ 0 π 2 sin x − cos x d x = − ∫ 0 π 4 sin x − cos x d x + ∫ π 4 π 2 sin x − cos x d x = − 2 ∫ 0 π 4 sin x − π 4 d x + ∫ π 4 π 2 sin x − π 4 d x S = 2 . cos x − π 4 π 4 0 − 2 . cos x − π 4 π 2 π 4 = 2 1 − 1 2 − 2 1 2 − 1 = 2 2 − 2 = 2 2 − 1
“Dùng CASIO tính tích phân trị tuyệt đối, dò đáp án
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x − 1 và đường thẳng y = 2.
A. 12
B. 4
C. 6
D. 2
Thể tích khối tròn khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = sin x cos x , y = 0 , x = 0 , x = π 2 là:
A. π 2 4
B. π 2 8
C. π 2 16
D. π 2 32
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 8 x + 1 và đường thẳng y = x + 2 .
A. 1 12
B. 1 6
C. 1 3
D. 1 2
Chọn B
Phương trình hoành độ giao điểm :

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - x + 1 và đường thẳng y = x + 4 .