Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia phân giác của B C D ^ .

Những câu hỏi liên quan
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C.
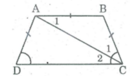
Ta có:
AB = AD (gt)
AD = BC (tính chất hình thang cân)
⇒ AB = BC do đó ΔABC cân tại B
⇒ ∠ BAC = ∠ BCA (tính chất tam giác cân) (*)
ABCD là hình thang có đáy là AB nên AB // CD
∠ BAC = ∠ DCA (hai góc so le trong) (**)
Từ (*) và (**) suy ra: ∠ BCA = ∠ DCA (cùng bằng ∠ BAC)
Vậy CA là tia phân giác của ∠ BCD.
Đúng 1
Bình luận (0)
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C ?
Ta có: \(AB = AD\)
Mà \(AD = BC\) (ABCD là hình thang cân)
\(\Rightarrow AB=BC\)
Nối A và C
Ta có: \(AB=BC\Rightarrow\Delta ABC\) là \(\Delta\) cân \(\Rightarrow\widehat{BAC}=\widehat{BCA}\) (1)
Ta lại có: AB // CD (ABCD là hình tang cân)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\) ( cặp góc so le trong) (2)
Từ (1) và (2) \(\Rightarrow\widehat{BCA}=\widehat{ACD}\Rightarrow CA\) là phân giác của \(\widehat{C}\) (ĐPCM)
Đúng 0
Bình luận (0)
Cau1: Cho hình thang cân ABCD có AB//CD. Gọi O là giao điểm của hai đường chéo, I là giao điểm của AD, BC. Chứng minh OI là trung trực của CD.
Câu2: Cho hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh CA là tia phân giác góc C.
2)
Có: \(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\AD=BC\left(2.cạnh.bên.hình.thang.cân\right)\end{matrix}\right.\)
\(\Rightarrow AB=BC\Rightarrow\Delta ABC.cân.tại.B\)
Mà AB // ED (gt)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
=> CA là tia phân giác của góc C.
Đúng 1
Bình luận (0)
: Hình thang cân ABCD, đáy nhỏ AB bằng cạnh bên AD. Chứng minh CA là tia phân giác góc C.
Ta có: AB=AD
mà AD=BC
nên BA=BC
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{BCA}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
Đúng 1
Bình luận (0)
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD.chứng minh rằng CA là tia phân giác của góc C
vì ABCD là hình thang cân nên ta có AD=BC(hai cạnh bên)
mà theo bài ra AB=AD => AB=AD=BC
=> tam giác ABC cân tại B => góc BAC= góc BCA(hai góc đáy)
mặt khác ta có góc BAC = góc ACD ( so le trong)
=> góc BCA = góc ADC => CA là tia phân giác góc C
Đúng 2
Bình luận (0)
hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C
mình cần ngay các bạn giúp mình với nhé !!!!!
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. CMR CA là tia phân giác của góc C.
Dễ mà
Ta có: AB = AD
Mà AD = BC ( vì ABCD là hình thang cân)
=> AB = BC
Nối A và C lại vs nhau
Ta có: AB = BC => tamm giác ABC là tam giác cân => góc BAC = góc BCA (1)
Ta lại có: AB // CD ( ABCD là hình tang cân)
=> Góc BAC = góc ACD ( cặp góc so le trong) (2)
Từ (1) và (2)
=> Góc BCA = góc ACD => CA là phân giác của góc C
Đúng 1
Bình luận (0)
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. C/m: CA là tia phân giác của góc C
Bài 1: Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tiaphân giác của BC · DBài 2: Cho hình thang cân ABCD (AB // CD, AB CD ). Gọi O là giao điểm của ADvà BC; Gọi E là giao điểm của AC và BD. Chứng minh:a) Tam giác AOB cân tại O;b) Các tam giác ABD và BAC bằng nhau;c) EC ED;d) OE là trung trực chung của AB và CD.Bài 3: Cho hình thang cân ABCD (AB // CD) có µ A C 2µ. Tính các góc của hình thang cânBài 4: Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạ...
Đọc tiếp
Bài 1: Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia
phân giác của BC · D
Bài 2: Cho hình thang cân ABCD (AB // CD, AB < CD ). Gọi O là giao điểm của AD
và BC; Gọi E là giao điểm của AC và BD. Chứng minh:
a) Tam giác AOB cân tại O;
b) Các tam giác ABD và BAC bằng nhau;
c) EC = ED;
d) OE là trung trực chung của AB và CD.
Bài 3: Cho hình thang cân ABCD (AB // CD) có µ A C 2µ. Tính các góc của hình thang cân
Bài 4: Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạnh bên
BC và đồng thời DB là tia phân giác của ADC.
a) Tính các góc của hình thang cân ABCD.
b) Biết BC = 6 cm, tính chu vi và diện tích của hình thang cân ABCD.


















