Trong mỗi đẳng thức sau, hãy tìm đa thức M phù hợp:
a) 3 y 2 + 6 y ( y − 1 ) M = 3 y y − 1 với y ≠ − 2 và y ≠ 1 ;
b) − 2 a 2 + 4 ab + 2 b 2 a + b = M b 2 − a 2 với a ≠ ± b .
Những câu hỏi liên quan
Hãy điền một đa thức thích hợp vào các chỗ trống trong mỗi đẳng thức sau:a)
2
a
3
+
4
a
2
a
2
−
4
.
..
a
−
2...
Đọc tiếp
Hãy điền một đa thức thích hợp vào các chỗ trống trong mỗi đẳng thức sau:
a) 2 a 3 + 4 a 2 a 2 − 4 = . .. a − 2 với a ≠ ± 2 ;
b) 5 ( x + y ) 3 = 5 x 2 − 5 y 2 . .. với x ≠ y .
Tìm đa thức B trong mỗi đẳng thức sau:a)
2
y
−
1
(
y
−
3
)
B
1
y
2
−
4
y
+
3
với
y...
Đọc tiếp
Tìm đa thức B trong mỗi đẳng thức sau:
a) 2 y − 1 ( y − 3 ) B = 1 y 2 − 4 y + 3 với y ≠ 1 2 ; y ≠ 1 và y ≠ 3 ;
b) a − 1 a 2 + 2 a + 4 = B a 3 − 8 và a ≠ 2 .
Trong mỗi đẳng thức sau, hãy tìm đa thức M:a)
3
x
2
−
2
x
−
5
M
3
x
−
5
2
x
−
3
với
x
≠
−...
Đọc tiếp
Trong mỗi đẳng thức sau, hãy tìm đa thức M:
a) 3 x 2 − 2 x − 5 M = 3 x − 5 2 x − 3 với x ≠ − 1 và x ≠ 3 2 ;
b) 2 x 2 + 3 x − 2 x 2 − 4 = M x 2 − 4 x + 4 với x ≠ ± 2 .
a) Kết quả M = (x + l)(2x - 3);
b) Kết quả M = (2x - 1)(x - 2).
Đúng 0
Bình luận (0)
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
4 x 2 - 3 x - 7 A = 4 x - 7 2 x + 3
⇒
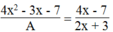4
x
2
-
3
x
-
7
2
x
+
3
=
A
4
x
-
7
⇒ 4 x 2 + 4 x - 7 x - 7 2 x + 3 = A 4 x - 7
⇒ [4x(x + 1) – 7(x + 1)](2x+ 3) = A(4x - 7)
⇒ (x + 1)(4x – 7)(2x + 3) = A(4x – 7)
⇒ A = (x + 1)(2x + 3) = 2 x 3 + 3 x + 2 x + 3 = 2 x 2 + 5 x + 3
Vậy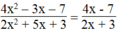 
Đúng 0
Bình luận (0)
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
x
2
-
2
x
2
x
2
-
3
x
-
2
x
2
+...
Đọc tiếp
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
x 2 - 2 x 2 x 2 - 3 x - 2 = x 2 + 2 x A
⇒
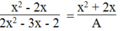x
2
-
2
x
.
A
=
2
x
2
-
3
x
-
2
x
2
+
2
x
⇒ x x - 2 . A = 2 x 2 - 4 x + x - 2 . x x + 2
⇒ x x - 2 . A = 2 x x - 2 + x - 2 . x x + 2
⇒ x(x – 2).A = (x – 2)(2x + 1).x.(x + 2)
⇒ A = (2x + 1)(x + 2) = 2 x 2 + 4 x + x + 2 = 2 x 2 + 5 x + 2
Vậy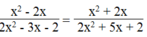 
Đúng 0
Bình luận (0)
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức :
x
+
2
P
x
-
2
x
-
1
Q
x
2...
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức : x + 2 P x - 2 = x - 1 Q x 2 - 4
x + 2 P x - 2 = x - 1 Q x 2 - 4
⇒ x + 2 . P . x 2 - 4 = x - 2 x - 1 . Q
Hay (x + 2)(x – 2)(x + 2).P = (x – 2)(x – 1).Q
Chọn P = (x – 1) thì Q = x + 2 2
Đúng 0
Bình luận (0)
Dùng tính chất cơ bản của phân thức, hãy điền một đa thức thích hợp vào các chỗ vào các chỗ trống trong mỗi đẳng thức sau:
.
.
.
.
.
x
-
y
3
x
2
-
3
x
y...
Đọc tiếp
Dùng tính chất cơ bản của phân thức, hãy điền một đa thức thích hợp vào các chỗ vào các chỗ trống trong mỗi đẳng thức sau: . . . . . x - y = 3 x 2 - 3 x y 3 y - x 2
3 y - x 2 = 3 . x - y 2 = x - y . 3 x - y
(Mẫu thức của phân thức bên trái bằng mẫu thức của phân thức bên phải chia cho 3(x – y)
Do đó ta chia cả tử và mẫu của phân thức bên phải cho 3(x – y) để thu được phân thức bên trái)
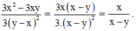
Vậy đa thức cần điền là x.
Đúng 0
Bình luận (0)
Dùng tính chất cơ bản của phân thức, hãy điền một đa thức thích hợp vào các chỗ vào các chỗ trống trong mỗi đẳng thức sau:
-
x
2
+
2
x
y
-
y
2
x
+
y
.
....
Đọc tiếp
Dùng tính chất cơ bản của phân thức, hãy điền một đa thức thích hợp vào các chỗ vào các chỗ trống trong mỗi đẳng thức sau: - x 2 + 2 x y - y 2 x + y = . . . . . . . y 2 - x 2
y 2 - x 2 = y - x y + x
(Mẫu thức của phân thức bên phải bằng mẫu thức của phân thức bên trái nhân với (y – x).
Do đó ta nhân cả tử và mẫu của phân thức bên trái với (y – x) để thu được phân thức bên phải)
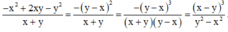
Vậy đa thức cần điền là x - y 3
Đúng 0
Bình luận (0)
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức:
x
+
2
.
P
x
2
-
1
x
-
2
.
Q...
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức: x + 2 . P x 2 - 1 = x - 2 . Q x 2 - 2 x + 1
x + 2 . P x 2 - 1 = x - 2 . Q x 2 - 2 x + 1
⇒ x + 2 . P . x 2 - 2 x + 1 = x 2 - 1 x - 2 . Q
Hay x + 2 x - 1 2 . P = x - 1 x + 1 x - 2 . Q
Chọn P = (x – 2)(x + 1) = x 2 - x - 2 thì Q = (x + 2)(x – 1) = x 2 + x - 2
Đúng 0
Bình luận (0)