Đặt \(MK=x\left(x>0\right)\)

Áp dụng định lý Pythagoras, ta được: \(x^2+QK^2=MQ^2\Rightarrow x^2=MQ^2-81\)(\(\Delta MKQ\)vuông tại K)

\(x^2+NK^2=MN^2\Rightarrow x^2=MN^2-256\)(\(\Delta MKN\)vuông tại K)

Từ đó suy ra \(2x^2=\left(MN^2+MQ^2\right)-337=NQ^2-337=288\Rightarrow x=12\)(Do x > 0)

\(\Rightarrow MN=\sqrt{12^2+16^2}=20cm\); \(MQ=\sqrt{12^2+9^2}=15cm\)

\(\Rightarrow P_{MNPQ}=\left(20+15\right).2=70\left(cm\right);S_{MNPQ}=20.15=300\left(cm^2\right)\)

b, vì MNPQ là hình chữ nhật => MN//NP

                                           => ˆMQN=ˆQNPMQN^=QNP^ (so le trong)

xét ΔMKQΔMKQ và ΔQPNΔQPN có  

  ˆMQN=ˆQNPMQN^=QNP^ (cmt)

   ˆMKQ=ˆNPQ=90oMKQ^=NPQ=90o^

=> ΔMKQΔMKQ đồng dạng với ΔQPNΔQPN (g.g)

=> MQNQ=MKQP(đpcm)MQNQ=MKQP(đpcm)

Trong hình chữ nhật MNPQ có: 

MN vuông góc với MQ;         MN vuông góc với NP;

PQ vuông góc với PN;            PQ vuông góc với QM.

Vậy hình chữ nhật MNPQ có 4 cặp cạnh vuông góc với nhau.

Đáp án đúng điền vào ô trống là 4

Bài 1:

Xét ΔMKQ có 

A là trung điểm của KM

B là trung điểm của KQ

Do đó: AB là đường trung bình của ΔMKQ

Suy ra: AB//MQ

a) Đoạn thẳng NP vuông góc với những đoạn thẳng Mn; Kh; PQ.

Dùng eke kiểm tra ta có :

+ Góc vuông là :

- Góc đỉnh M, cạnh MN, MQ.

- Góc đỉnh Q, cạnh QP, QM.

+ Các góc không vuông là :- Góc đỉnh N, cạnh NM, NP

- Góc đỉnh P, cạnh PQ, PN.

Dùng eke kiểm tra ta có :

+ Góc vuông là :

- Góc đỉnh M, cạnh MN, MQ.

- Góc đỉnh Q, cạnh QP, QM.

+ Các góc không vuông là :- Góc đỉnh N, cạnh NM, NP

- Góc đỉnh P, cạnh PQ, PN.

Chọn B

b

B

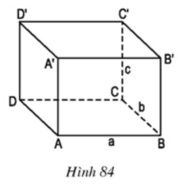
- A’A có vuông góc với AD vì là hai cạnh kề nhau của hình chữ nhật AA’D’D

- A’A có vuông góc với AB vì là hai cạnh kề nhau của hình chữ nhật AA’B’B