Giải các hệ phương trình sau bằng phương pháp cộng đại số:
a ) 3 x + y = 3 2 x − y = 7 b ) 2 x + 5 y = 8 2 x − 3 y = 0 c ) 4 x + 3 y = 6 2 x + y = 4 d ) 2 x + 3 y = − 2 3 x − 2 y = − 3 e ) 0 , 3 x + 0 , 5 y = 3 1 , 5 x − 2 y = 1 , 5
Những câu hỏi liên quan
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
2
x
+
3
y
-
2
3
x
-
2
y...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 2 x + 3 y = - 2 3 x - 2 y = - 3
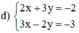
(Nhân hai vế pt 1 với 2, pt 2 với 3 để hệ số của y đối nhau)
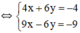(Hệ số của y đối nhau nên cộng từng vế hai phương trình).
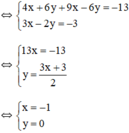
Vậy hệ phương trình có nghiệm duy nhất (-1; 0).
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3
,
3
x
+
4
,
2
y
1
9
x
+
14...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3 , 3 x + 4 , 2 y = 1 9 x + 14 y = 4
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3
x
-
2
y
10
x
-
2
3
y
3...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3 x - 2 y = 10 x - 2 3 y = 3 1 3
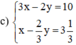(Nhân hai vế pt 2 với 3 để hệ số của y bằng nhau)
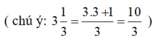
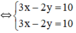(Trừ từng vế hai phương trình)
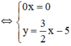
Phương trình 0x = 0 nghiệm đúng với mọi x.
Vậy hệ phương trình có vô số nghiệm dạng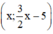 
(x ∈ R).
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
4
x
+
7
y
16
4
x
-
3
y
-
24
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 4 x + 7 y = 16 4 x - 3 y = - 24
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3
x
+
y
3
2
x
-
y
7
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3 x + y = 3 2 x - y = 7
(Các phần giải thích học sinh không phải trình bày).
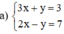(Vì hệ số của y ở 2 pt đối nhau nên cộng từng vế của 2 pt).
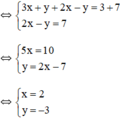
Vậy hệ phương trình có nghiệm duy nhất (2; -3).
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
10
x
-
9
y
8
15
x
+
21
y
0
,...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 10 x - 9 y = 8 15 x + 21 y = 0 , 5
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
2
x
+
2
3
y
5
3
2
x
-...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 2 x + 2 3 y = 5 3 2 x - 3 y = 9 2
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
5
x
3
+
y
2
2
x
6
-...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 5 x 3 + y = 2 2 x 6 - y 2 = 2
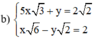(Chia hai vế pt 2 cho √2 để hệ số của y đối nhau)
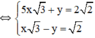(Hệ số của y đối nhau nên cộng từng vế của 2 pt)
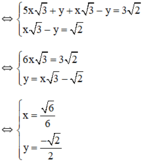
Vậy hệ phương trình có nghiệm duy nhất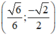 
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
x
2
-
3
y
1
2
x
+
y
2...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: x 2 - 3 y = 1 2 x + y 2 = - 2
(Các phần giải thích học sinh không phải trình bày).
(Chia hai vế của pt 2 cho √2 để hệ số của x bằng nhau)
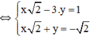(Trừ từng vế của hai phương trình)
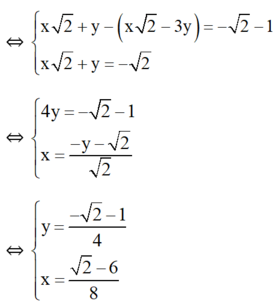
Vậy hệ phương trình có nghiệm duy nhất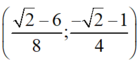 
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
2
x
-
11
y
-
7
10
x
+
11
y...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 2 x - 11 y = - 7 10 x + 11 y = 31
