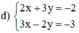
(Nhân hai vế pt 1 với 2, pt 2 với 3 để hệ số của y đối nhau)
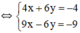 (Hệ số của y đối nhau nên cộng từng vế hai phương trình).
(Hệ số của y đối nhau nên cộng từng vế hai phương trình).
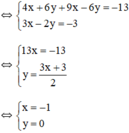
Vậy hệ phương trình có nghiệm duy nhất (-1; 0).
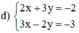
(Nhân hai vế pt 1 với 2, pt 2 với 3 để hệ số của y đối nhau)
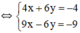 (Hệ số của y đối nhau nên cộng từng vế hai phương trình).
(Hệ số của y đối nhau nên cộng từng vế hai phương trình).
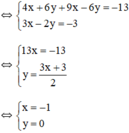
Vậy hệ phương trình có nghiệm duy nhất (-1; 0).
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 5 x 3 + y = 2 2 x 6 - y 2 = 2
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
a ) x 2 − 3 y = 1 2 x + y 2 = − 2 b ) 5 x 3 + y = 2 2 x 6 − y 2 = 2
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3 x + y = 3 2 x - y = 7
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 4 x + 3 y = 6 2 x + y = 4
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x + y 5 = 0 x 5 + 3 y = 1 − 5 b ) ( 2 − 3 ) x − 3 y = 2 + 5 3 4 x + y = 4 − 2 3
Giải hệ phương trình bằng phương pháp cộng đại số:
a) (\(\hept{\begin{cases}\left(x+2\right)\left(y-2\right)=x.y\\\left(x+y\right)\left(y-3\right)=x.y+6\end{cases}}\)
b)\(\hept{\begin{cases}\frac{x+1}{x-1}=\frac{y+3}{x-1}\\3x+2y=-2\end{cases}}\)
a ) \(\frac{x}{2x+2}-\frac{2x}{x^2-2x-3}=\frac{x}{6-2x}\)
b ) Dùng phương pháp thế hoặc phương pháp cộng đại để giải hệ phương trình sau :
\(\hept{\begin{cases}\sqrt{2}x-3y=2006\\2x+\sqrt{3}y=2007\end{cases}}\)
Giải các hệ phương trình sau bằng phương pháp cộng đại số: x 2 - 3 y = 1 2 x + y 2 = - 2
Giải hệ phương trình sau (bằng cách cộng đại số):
5/ \(\left\{{}\begin{matrix}\left(x-2\right)^2-2y^3=6\\3\left(x-2\right)^2+5y^3=7\end{matrix}\right.\)