Cho I, O lần lượt là tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC với A ^ = 60 0 . Gọi H là trực tâm của ∆ABC. Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn

Những câu hỏi liên quan
Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với A = 60 ° . Gọi H là giao điểm của các đường cao BB'và CC'.
Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
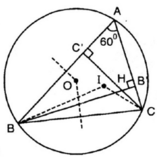

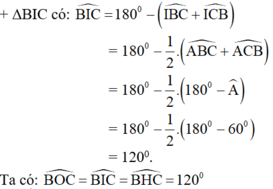
⇒ B, O, I, H, C cùng thuộc đường tròn chứa cung 120º dựng trên đoạn BC.
Kiến thức áp dụng
+ Các điểm cùng nhìn một đoạn thẳng cố định dưới cùng một góc α thì đều thuộc cùng một đường tròn.
Đúng 0
Bình luận (0)
Cho tam giác ABC có A bằng 60 độ .Các điểm O,I lần lượt là tâm đường tròn ngoại tiếp tam giác và nội tiếp tam giác.Chứng mình B,O,I,C cùng thuộc một đường tròn
Vì \(\widehat{BAC}=60^o\Rightarrow\widehat{ABC}+\widehat{ACB}=120^o\)
Mà BI,CI là tia phân giác góc \(\widehat{ABC},\widehat{ACB}\)
\(\Rightarrow\widehat{IBC}+\widehat{ICB}=60^o\Rightarrow\widehat{BIC}=180^o-60^o=120^o\)
\(\widehat{BAC}=\frac{1}{2}sđ\widebat{BC}=60^o\Rightarrow sđ\widebat{BC}=120^o\)
Mà \(\widehat{BOC}=sđ\widebat{BC}=120^o\)
\(\Rightarrow\widehat{BIC}=\widehat{BOC}=120^o\)
Suy ra tứ giác BIOC nội tiếp hay B,O,I,C cùng thuộc 1 đường tròn
Cho tam giác ABC có góc A=600.Các điểm O,I lần lượt là tâm đường tròn ngoại tiếp,nội tiếp tam giác.Chứng minh rằng bốn điểm B,O,I,C cùng thuộc một đường tròn.
Câu hỏi của Lê Thanh Bình - Toán lớp 9 - Học toán với OnlineMath
bạn tham khảo
Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với \(\widehat{A}=60^o.\) Gọi H là giao điểm của các đường cao BB' và CC'. Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
Ta có: = 2
= 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và =
(đối đỉnh)
mà = 180o -
= 180o - 60o = 120o
nên = 120o (2)
=
+
= 60o + = 60o+ 60o
(sử dụng góc ngoài của tam giác)
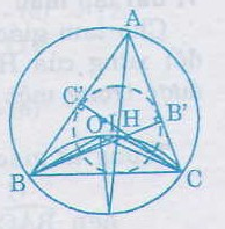
Do đó = 120o
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn
Đúng 0
Bình luận (0)
Ta có: \(\widehat{BOC}\) = 2\(\widehat{BAC}\) = 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và \(\widehat{BHC}\) = \(\widehat{B'HC'}\) (đối đỉnh)
mà \(\widehat{B'HC'}\) = 180o - \(\widehat{A}\) = 180o - 60o = 120o
nên \(\widehat{BHC}\) = 120o (2)
\(\widehat{BIC}\) = \(\widehat{A}\) + \(\dfrac{\widehat{B}+\widehat{C}}{2}\)
= 60o + \(\dfrac{180^0-60^0}{2}\) = 60o+ 60o
(sử dụng góc ngoài của tam giác)

Do đó \(\widehat{BIC}\) = 120o
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn
Đúng 0
Bình luận (0)
Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với A = 60 o . Gọi H là giao điểm của các đường cao BB'và CC'.
Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
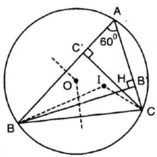

![]() (hai góc đối đỉnh)
(hai góc đối đỉnh)
![]()
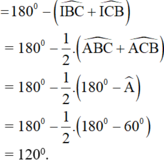
![]()
⇒ B, O, I, H, C cùng thuộc đường tròn chứa cung 120º dựng trên đoạn BC.
Đúng 0
Bình luận (0)
ho tam giác abc nội tiếp đường tròn (o,r) goi I là tâm của đường tròn nội tiếp tam giác đó gọi M N P lần lượt là tâm của các đường tròn bàng tiếp trong các góc A, B, C. gọi K là điểm đối xứng của I qua O. Chứng minh rằng K laftaam đường tròn ngoại tiếp tam giác MNP
cách làm thôi nha
GỌi D là gia điểm của AM zới đường tròn (O)
CM các tam giác DBI . DBM cân
=> DI=DM
DO đó OD là đường trung bình của tam giác MIK
=> KM=2OD=2R
Zậy M thuộc đường tròn (K;2R)
tương tự đối zới các điểm N , P
Cho tam giác ABC cân tại A có O,I,P lần lượt là tâm đường tròn ngoại tiếp,nội tiếp và bàng tiếp góc A.Từ P kẻ tiếp tuyến với đường tròn ngoại tiếp tam giác PBC cắt tia AB,AC lần lượt tại M,N.Chứng minh rằng (MPB);(NPC);(ABC);AI;AP đồng quy tại một điểm
Sửa đề : (NPB);(MPC);(ABC);AI;AP đồng quy
Cho tam giác ABC , D là điểm trên cạnh BC sao cho đường tròn nội tiếp tam giác ABD và tam giác ADC tiếp xúc nhau tại một điểm thuộc cạnh AD. Gọi I, J lần lượt là tâm đường tròn nội tiếp tam giác ABD và tam giác ADC , O là tâm đường tròn ngoại tiếp tam giác AIJ
a) Xác định vị trí điểm D trên cạnh BC
b) Từ câu a) chứng minh rằng đường phân giác góc BAC qua tâm O
Cho tam giác ABC , D là điểm trên cạnh BC sao cho đường tròn nội tiếp tam giác ABD và tam giác ADC tiếp xúc nhau tại một điểm thuộc cạnh AD. Gọi I, J lần lượt là tâm đường tròn nội tiếp tam giác ABD và tam giác ADC , O là tâm đường tròn ngoại tiếp tam giác AIJ
a) Xác định vị trí điểm D trên cạnh BC
b) Từ câu a) chứng minh rằng đường phân giác góc BAC qua tâm O














