ý B tk cho mk nha

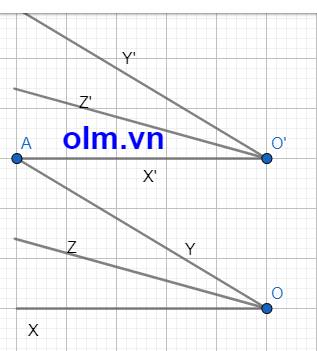
a,Kéo dài OY cắt O'X' tại A ta có: 

  \(\widehat{XOY}\) =  \(\widehat{XOA}\)  = \(\widehat{OAO'}\) (so le trong) (1)

   \(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)

Kết hợp (1) Và (2) ta có:

    \(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)

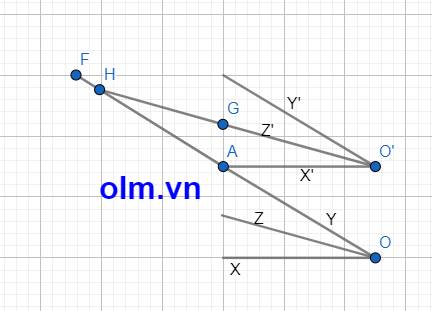
b, Kéo dài OY cắt O'Z' tại H 

             \(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY

             \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')

         Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)

               \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\)  ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)

          ⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)

         ⇒ OZ // O'Z' (đpcm)

Vì AOB và BOC là hai góc kề nhau

=> tia OB nằm giữa hai tia OA và OC

=> AOC = AOB + BOC

Mà2AOB = 3BOC

=> AOB = 3/2BOC

vì AOC = 150(o)

=> 150(o) = AOB + 3/2AOB

                 = 5/2AOB

=>AOB = 150(o) : 5/2

             = 60(o)

=>BOC = 3/2.60(o)

             = 90(o)

Vậy AOC = 60(o) , BOC = 90(o)

Ta có: 2AOB=3BOC

=> AOB=2/3BOC

mà AOB+BOC=150 độ

=>2/3BOC+BOC=150 độ

=>BOC(2/3+1)=150độ

=>5/3BOC=150 độ

=>BOC=150độ : 5/3

=> BOC=150độ*3/5

=>BOC= 90 độ

=>AOB=150độ-90độ=60 độ

Đ/Số: AOB=60 độ

         BOC=90 độ

Ta có \(2\widehat{AOB}\) = \(\widehat{3BOC}\)

    => \(2\widehat{AOB}\)\(-\) \(\widehat{3BOC}\)= \(0\)

   =>\(2\widehat{AOB}\) +2\(\widehat{BOC}\) - \(\widehat{5BOC}\) = 0

  => 2(\(\widehat{AOB}\)+\(\widehat{BOC}\)) - \(\widehat{5BOC}\) = 0

 => 2x150 \(-\)\(\widehat{5BOC}\)= 0

=> 300 - \(\widehat{5BOC}\)=0

=> \(\widehat{5BOC}\)= 300

=>\(\widehat{BOC}\)= 300 : 5

=> \(\widehat{BOC}\)= 60

 Ta có \(\widehat{AOB}\)+ \(\widehat{BOC}\)= 150

         \(\widehat{AOB}\)+ 60 =150 

        \(\widehat{AOB}\) = 150 - 60 =90

Vậy \(\widehat{AOB}\)=90 độ

       \(\widehat{BOC}\)=60 độ

a)góc yot =60 độ    b)ko,vì xot và yot ko = nhau    

khó quá bạn ạ