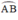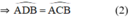Tứ giác ABCD nội tiếp một đường tròn và góc C ^ = 75 0 . Khẳng định nào sau đây đúng.
a, A ^ = 105 0
b, B ^ = 75 0
c, C ^ = 90 0
d, D ^ = 75 0
Cho tứ giác ABCD nội tiếp trong đường tròn biết A^ = 75 độ ; B= 60 độ . Tình số đo góc C và góc D
Vì tứ giác ABCD nội tiếp (O)
=> góc B + góc C = 180 độ (tổng 2 góc đối bằng 180 độ)
=> 60 + góc C = 180
=> góc C = 180 - 60 = 120 độ
Tiếp tục, ta cũng có góc A + góc D = 180 độ
=> 75 + góc D = 180
=> góc D = 180 - 75 = 105 độ
Note: Bài này đoạn kết còn có cách tính khác, cần inbox mình
Theo mk thi: goc C=105° va goc D=120°
Aj thay dung thj ung ho mk nha!!! Cam on.
Ban Vu Nhu Mai ve hinh nhu the thi se la tu giac ABDC ( saj de bai)
De bai la tu giac ABCD .
Cho tứ giác ABCD nội tiếp đường tròn tâm O đường kính AD hai đường chéo AC và BD cắt nhau tại E kẻ EF vuông góc ad a) Chứng minh tứ giác ECDF nội tiếp Xác định tâm I b) Chứng minh CA là phân giác của góc BCF c) Chứng minh tứ giác bcef nội tiếp
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Cho tứ giác lồi ABCD. CMR nếu tồn tại một đường tròn nội tiếp tứ giác và một đường tròn tiếp xúc với các cạnh kéo dài của nó thì:
a) AB+DC=AD+BC
b) AB-DC=AD-BC
c) Các đường chéo của tứ giác vuông góc với nhau.
cho tứ giác ABCD nội tiếp đường tròn tâm (O) đường kính AB. Hai đường chéo AC và BD cắt nhau tại I. Kẻ IE vuông góc với AB. Chứng minh rằng:
a) Tứ giác AIDE nội tiếp một đường tròn.
b) Tia BD là tia phân giác của góc CDE.
c) Trường hợp AB không song song với CD. Chứng minh 4 điểm O, E, D, C cùng thuộc một đường tròn.
Cô hướng dẫn nhé. :)
Tứ giác AIDE nội tiếp đường tròn đường kính AI.
b. Do câu a ta có AIDE là tứ giác nội tiếp nên gó IDE = góc IAE. Lại có góc IAE = góc CDB. Từ đó suy ra DB là tia phân giac góc CDE.
c. Ta thấy góc CDE = 2 góc CAB (Chứng minh b). Lại có góc COB = 2 góc CAB. Từ đó suy ra góc CDE = góc COB. Hay OEDC là tứ giác nội tiếp ( Góc ngoài ở đỉnh bằng góc đối diện )
Chúc em học tốt ^^
Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính AB. Hai đường chéo AC và BD cắt nhau tại I. Kẻ IE vuông góc với AB. Chứng minh :
a. Tứ giác ADIE nội tiếp đường tròn ;
b. Tia DB là phân giác của góc CDE ;
c. Nếu AB không song song CD, chứng minh bốn điểm O, E, D, C cùng thuộc một đường tròn.
tứ giác ABCD nội tiếp đường tròn đường kính AD.Hai đường chéo AB và CD cắt nhau tại E, và F vuông góc với AD ( F thuộc AD). Chứng minh tứ giác DCEF nội tiếp
Sửa đề: Hai đường chéo BD và AC cắt nhau tại E
góc ACD=1/2*sđ cung AD=90 độ
góc EFD+góc ECD=180 độ
=>EFDC nội tiếp
Cho △ ABC vuông tại A, với AC > AB. Trên AC lấy một điểm M, vẽ đường tròn (O) đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S
a. Chứng minh ABCD là tứ giác nội tiếp.
B. Chứng minh góc ABD = góc ABD
C. Chứng minh CA là tia phân giác của góc. AOB bằng 75°
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc AD tại F. Gọi M là trung điểm DE. Chứng minh:
a) Các tứ giác ABEF, DCEF nội tiếp
b) CA là phân giác góc BCF
c) Tứ giác BCMF nội tiếp
Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
a) ABCD là một tứ giác nội tiếp
b) góc ABD bằng góc ACD
c) CA là tia phân giác của góc SCB
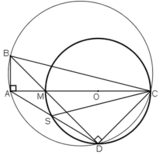
a) 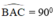 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC

⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
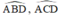 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 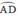
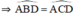
c) + Trong đường tròn đường kính MC:
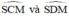 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 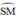
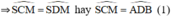
+ Trong đường tròn đường kính BC:
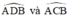 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung