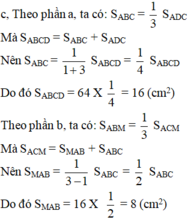Chìnhinh thang ABCD, đáy AB = 1/3 DC. Kéo dài DA và CB cắt nhau tại O. Diện tích AOB là 5 cm2 . Tinh diện tích hình thang ABCD.

Những câu hỏi liên quan
Cho hình thang ABCD,đáy AB = 1/3 DC.Kéo dài DA và CB cắt nhau tại O.Diện tích tích tam giác AOB = 5 cm2.Tính diện tích hình thang ABCD
Giải đầy đủ và dễ hiểu nhé
đề giống mình thế đáp án là 64 cm2 chắc chắn đúng
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho hình thang abcd có đáy ab = 1/3 cd . kéo dài da về phía a và cb về phía b chúng cắt nhau tại g . tính diện tích hình thang abcd biết diện tích hình tam giác abg là 11 cm2
Cho hình thang abcd có hai đáy là ab và dc.biết dc=ab*3.kéo dài hai cạnh bên là da và cb cắt nhau tại g.Tính diện tích hình thang abcd biết rằng diện tích hình tam giác gab là 6 cm 2
cho hình thang ABCD có diện tích bằng 16cm2 dây AB bằng 1/3 đáy lớn DC . kéo dài DA và CB cắt nhau tại M . tính diện tích AMB
bài này khó quá,minh ko biết làm,kết bạn mình nhé
Đúng 0
Bình luận (0)
\(\frac{ }{\frac{ }{ }\frac{ }{ }\frac{ }{ }}\)Thằng LHM xàm thế âm điểm là phải rồi ^.^
Đúng 0
Bình luận (0)
mình không chắc chắn lắm đau nhà hihi...........................
Xét tam giác ABC và ACD có cùng chiều cao chính là chiều cao hình thang, đáy dc gấp 3 đáy AB => S_ACD gấp 3 lần S_ABC.
Vậy diện tích tam giác ABC là: 16 : (3 + 1) = 4 (cm2)
Xét tam giác MAB và MAC có chung đáy MA mà CD gấp 3 lần AB (vì AB và CD cùng vuông góc với MD ) =>S_MAB = 1/3 S_MAC => S_MAB =1/2 S_ABC
Vậy diện tích MAB là: 4:(3-1)=2(cm2)
Đúng 0
Bình luận (0)
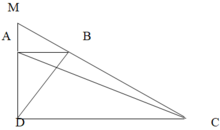
Cho hình thang vuông ABCD vuông góc tại A và D; AB = 1 3 CD. Kéo dài DA và CB cắt nhau tại M.
c) Diện tích hình thang ABCD bằng 64 cm2.Tính diện tích tam giác MBA .
Cho hình thang vuông ABCD có diện tích bằng 20 cm2 AB=1/3 CĐN kéo dài DA và CB cắt nhau tại M. Tính diện tích tam giác MAB.
Hai tg ABC và tg ACD có đường cao từ C->AB = đường cao từ A->CD nên
\(\dfrac{S_{ABC}}{S_{ACD}}=\dfrac{AB}{CD}=\dfrac{1}{3}\Rightarrow S_{ACD}=3xS_{ABC}\)
\(\Rightarrow S_{ABCD}=S_{ABC}+S_{ACD}=S_{ABC}+3xS_{ABC}=4xS_{ABC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{4}xS_{ABCD}\)
Kéo dài AB, từ C dựng đường thẳng song song với AD cắt AB kéo dài tại E => AECD là hình chữ nhật
\(\Rightarrow AE=CD\Rightarrow AB=\dfrac{1}{3}CD=\dfrac{1}{3}AE\Rightarrow AB=\dfrac{1}{2}xBE\)
Hai tg ABC và tg EBC có chung đường cao từ C->AB nên
\(\dfrac{S_{ABC}}{S_{EBC}}=\dfrac{AB}{BE}=\dfrac{1}{2}\)
Hai tg này có chung BC nên
\(\dfrac{S_{ABC}}{S_{EBC}}=\) đường cao từ A->BC = đường cao từ E->BC\(=\dfrac{1}{2}\)
Hai tg AMC và tg EMC có chung MC nên
\(\dfrac{S_{AMC}}{S_{EMC}}=\)đường cao từ A->BC = đường cao từ E->BC\(=\dfrac{1}{2}\)
Hai tg AMC và tg AME có chung AM và đường cao từ C->AD = đường cao từ E->AD nên
\(S_{AMC}=S_{AME}\Rightarrow\dfrac{S_{AME}}{S_{EMC}}=\dfrac{1}{2}\)
Hai tg AME và tg EMC có đường cao từ C->AD = đường cao từ M->EC nên
\(\dfrac{S_{AME}}{S_{EMC}}=\dfrac{AM}{EC}=\dfrac{1}{2}\)
Hai tg MAB và tg ABC có chung AB nên
\(\dfrac{S_{MAB}}{S_{ABC}}=\) đường cao từ A->AB / đường cao từ C->AB = \(\dfrac{AM}{EC}=\dfrac{1}{2}\)
\(\Rightarrow S_{MAB}=\dfrac{1}{2}xS_{ABC}=\dfrac{1}{2}x\dfrac{1}{4}xS_{ABCD}=\dfrac{1}{8}xS_{ABCD}=2,5cm^2\)
Đúng 2
Bình luận (0)
:Hình thang ABCD,đáy bé AB = 3/7 đáy lớn DC,diện tích tam giác AOB = 15,6 cm2.Tính diện tích hình thang ABCD?(AC cắt BD tại O)
Xem chi tiết
cho hình thang ABCD có đáy AB = 2/5 DC . So sánh diện tích tam giác ABD và CBD . KÉO DÀI DA và CB cắt nhau tại M . So sánh MB và BC
cho hình thang ABCD có cạnh đáy AB = một nửa DC. Kéo dài DA và CB cắt nhau tại điểm E.So sánh diện tích DBE và DBC