Biết rằng hệ phương trình: x 2 + y 2 + 2 x y = 8 2 x + y = 4 có nghiệm duy nhất (x; y). Tính x y
A. 3
B. 1 2
C. 2
D. 1
Cho hệ phương trình 2 x + b y = − 4 b x − a y = − 5 . Biết rằng hệ phương trình có nghiệm là (1; −2). Tính a + b
A. −1
B. 1
C. 2
D. −7
Thay x = 1; y = −2 vào hệ ta được 2 + b ( − 2 ) = − 4 b − a ( − 2 ) = − 5
Ta coi đây là một hệ phương trình bậc nhất hai ẩn là a và b và giải hệ phương trình này
2 + b ( − 2 ) = − 4 b − a ( − 2 ) = − 5 ⇔ − 2 b = − 6 b + 2 a = − 5 ⇔ b = 3 3 + 2. a = − 5 ⇔ b = 3 a = − 4
Suy ra a + b = −4 + 3 = −1
Đáp án: A
Cho hệ phương trình 2 x + b y = − 1 b x − 2 a y = 1 . Biết rằng hệ phương trình có nghiệm là (1; −2). Tính a – b
A. 13 8
B. − 13 8
C. 5 8
D. − 5 8
Thay x = 1; y = −2 vào hệ ta được:
2.1 + b . ( − 2 ) = − 1 b .1 − 2 a . ( − 2 ) = 1 ⇔ − 2 b = − 3 b + 4 a = 1 ⇔ b = 3 2 3 2 + 4 a = 1 ⇔ b = 3 2 a = − 1 8 ⇒ a − b = − 13 8
Vậy a – b = − 13 8
Đáp án: B
Cho hệ phương trình: a(x2 + y2)+ x + y = b và y - x= b biết rằng hệ có nghiệm với mọi b . C hứng minh rằng a=0
Cho hệ phương trình x 2 - y 3 = 1 x + y 3 = 2 . Biết nghiệm của hệ phương trình là (x; y), tính x + 3 3 y
A. 3 2 + 2
B. - 3 2 - 2
C. 2 2 - 2
D. 3 2 - 2
Cho hệ phương trình x 2 - y 3 = 1 x + y 3 = 2 . Biết nghiệm của hệ phương trình là (x; y), tính x + 3 3 y
A. 3 2 + 2
B. - 3 2 - 2
C. 2 2 - 2
D. 3 2 - 2
Cho hệ phương trình x 2 − y 3 = 1 x + y 3 = 2 . Biết nghiệm của hệ phương trình là (x; y), tính x + 3 3 y
A. 3 2 + 2
B. - 3 2 - 2
C. 2 2 - 2
D. 3 2 - 2
Ta có
x 2 − y 3 = 1 x + y 3 = 2 ⇔ x 2 − y 3 = 1 x 2 + y 6 = 2 ⇔ x 2 − y 3 = 1 6 + 3 y = 1 ⇔ x 2 − y 3 = 1 y = 1 6 + 3 ⇔ y = 6 − 3 3 x 2 − 3 . 6 − 3 3 = 1 ⇔ y = 6 − 3 3 x = 1
Vậy hệ đã cho có nghiệm duy nhất ( x ; y ) = 1 ; 6 − 3 3
Đáp án: D
a) Xác định các hệ số a và b, biết rằng hệ phương trình 2 x + b y = − 4 b x − a y = − 5 có nghiệm (1 ; -2).
b) Cũng hỏi như vậy nếu phương trình có nghiệm là (√2 - 1; √2)
a) Hệ phương trình 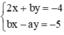 có nghiệm (1 ; -2) khi và chỉ khi (1;-2) thỏa mãn hệ phương trình. Thay x = 1, y = -2 vào hệ phương trình ta được:
có nghiệm (1 ; -2) khi và chỉ khi (1;-2) thỏa mãn hệ phương trình. Thay x = 1, y = -2 vào hệ phương trình ta được:
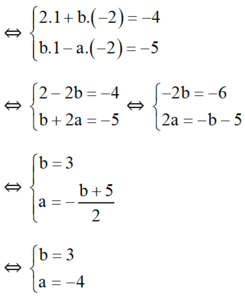
Vậy với a = -4 và b = 3 thì hệ phương trình nhận (1; -2) là nghiệm.
b) Hệ phương trình 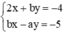 có nghiệm (√2 - 1; √2)khi và chỉ khi (√2 - 1; √2)thỏa mãn hệ phương trình.Thay (√2 - 1; √2)vào hệ phương trình ta được:
có nghiệm (√2 - 1; √2)khi và chỉ khi (√2 - 1; √2)thỏa mãn hệ phương trình.Thay (√2 - 1; √2)vào hệ phương trình ta được:
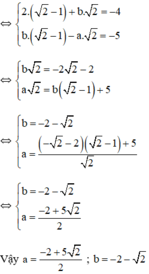
cho hệ phương trình \(\left\{{}\begin{matrix}x+y=2\\\left(m+1\right)x+my=7\end{matrix}\right.\)
a) chứng minh rằng: với mọi m thì hệ phương trình luôn có nghiệm x,y thỏa mãn x.y =< 1
b) tìm m là số nguyên để hệ phương trình có nghiệm thỏa mãn x.y>0
Lời giải:
a.
Từ $x+y=2\Rightarrow y=2-x$. Thay vào PT(2):
$(m+1)x+m(2-x)=7$
$\Leftrightarrow x+2m=7$
$\Leftrightarrow x=7-2m$
$y=2-x=2-(7-2m)=2m-5$
Vậy hpt có nghiệm $(x,y)=(7-2m, 2m-5)(*)$
Nếu $x,y$ có 1 số $\geq 0$, một số $\leq 0$ thì $xy\leq 0< 1$
Nếu $x,y$ cùng $\geq 0$ thì áp dụng BĐT Cô-si:
$2=x+y\geq 2\sqrt{xy}\Rightarrow xy\leq 1$
Vậy tóm lại $xy\leq 1(**)$
Từ $(*); (**)$ suy ra với mọi $m$ thì hpt luôn có nghiệm $x,y$ thỏa mãn $xy\leq 1$
b.
$xy>0$
$\Leftrightarrow (7-2m)(2m-5)>0$
$\Leftrightarrow 7> 2m> 5$
$\Leftrightarrow \frac{7}{2}> m> \frac{5}{2}$
Do $m$ nguyên nên $m=3$
Thử lại thấy đúng.
Cho hệ phương trình 4 x - 3 y = 4 2 x + y = 2 . Biết nghiệm của hệ phương trình (x; y) , tính x.y
A. 2
B. 0
C. -2
D. 1
Cho hệ phương trình 4 x - 3 y = 4 2 x + y = 2 . Biết nghiệm của hệ phương trình (x; y) , tính x.y
A. 2
B. 0
C. -2
D. 1