Cho tứ diện đều ABCD cạnh a. Tính diện tích mặt cầu nội tiếp tứ diện ABCD
A. πa 2 4
B. πa 2 6
C. Đáp án khác
D. 2 πa 2 3
Cho tứ diện đều ABCD cạnh a. Tính diện tích mặt cầu nội tiếp tứ diện ABCD.
A. 2 πa 2 3
B. πa 2 6
C. πa 2 4
D. Đáp án khác
Tứ diện ABCD là tứ diện đều nội tiếp trong mặt cầu bán kính R. Tính độ dài của cạnh tứ diện đều theo R
A. R 2
B. R 3
C. 2 R 2 3
D. R 6 2
Đáp án C
Đặt AB = x, M, N lần lượt là trung điểm AB, CD, I là trung điểm MN thì I là tâm mặt cầu, có
![]()
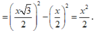
![]()
![]()
Cho tứ diện ABCD có CD=a 2 , ∆ ABC là tam giác đều cạnh a, ∆ ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng
T = M A 2 + M B 2 + M C 2 + M D 2
A. 3 a 2 8
B. a 2
C. 4 a 2
D. 2 a 2
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng T = M A 2 + M B 2 + M C 2 + M D 2 .
A. 3 a 2 8
B. a 2
C. 4 a 2
D. 2 a 2
Đáp án D
Với tứ diện đều ABCD thì mặt cầu (S) là mặt cầu có tâm trùng với tâm của mặt cầu ngoại tiếp tứ diện ABCD và là trọng tâm của tứ diện đều cạnh a, đồng thời có bán kính R = a 2 4
Gọi G là trọng tâm của tứ diện ⇒ G A ¯ + G B ¯ + G C ¯ + G D ¯ = 0 ¯
Ta có:
T = M A 2 + M B 2 + M C 2 + M D 2 = M G ¯ + G A ¯ 2 + M G ¯ + G B ¯ 2 + M G ¯ + G C ¯ 2 + M G ¯ + G D ¯ 2
= 4 M G 2 + 2 M G ¯ G A ¯ + G B ¯ + G C ¯ + G D ¯ ⏟ 0 + G A 2 + G B 2 + G C 2 + G D 2 = 4 M G 2 + 4 G A 2
= 4 a 2 4 2 + 4 a 6 4 2 = 2 a 2 . Vậy T = M A 2 + M B 2 + M C 2 + M D 2 = 2 a 2
Cho tứ diện ABCD có C D = a 2 , ∆ A B C là tam giác đều cạnh a, ∆ A C D vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng
A. 4 πa 3 3
B. πa 3 6
C. 4 πa 3
D. πa 3 3 2
Chọn A
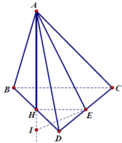
Coi như a = 1 . Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ B C D và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ A H E ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 πa 3
Cho tứ diện ABCD có C D = a 2 , Δ A B C là tam giác đều cạnh a, Δ A C D vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng
A . 4 π a 3 3 .
B . π a 3 6 .
C . 4 π a 3 .
D . π a 3 3 2 .
Chọn A
Coi như a =1. Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B ⇒ Δ A B D cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ ( B C D ) và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ ( A H E ) ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có
A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 π
Cho tứ diện ABCD có AB=2, CD=4 và các cạnh còn lại cùng bằng 6. Tính diện tích mặt cầu ngoại tiếp tứ diện S.ABCD
![]()
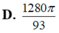
Cho tứ diện ABCD có AB=2; CD=4 và các cạnh còn lại cùng bằng 6. Tính diện tích mặt cầu ngoại tiếp tứ diện S.ABCD.
A. 1156 π 31
B. 1156 π 93
C. 47 π
D. 1280 π 93
Đán án C
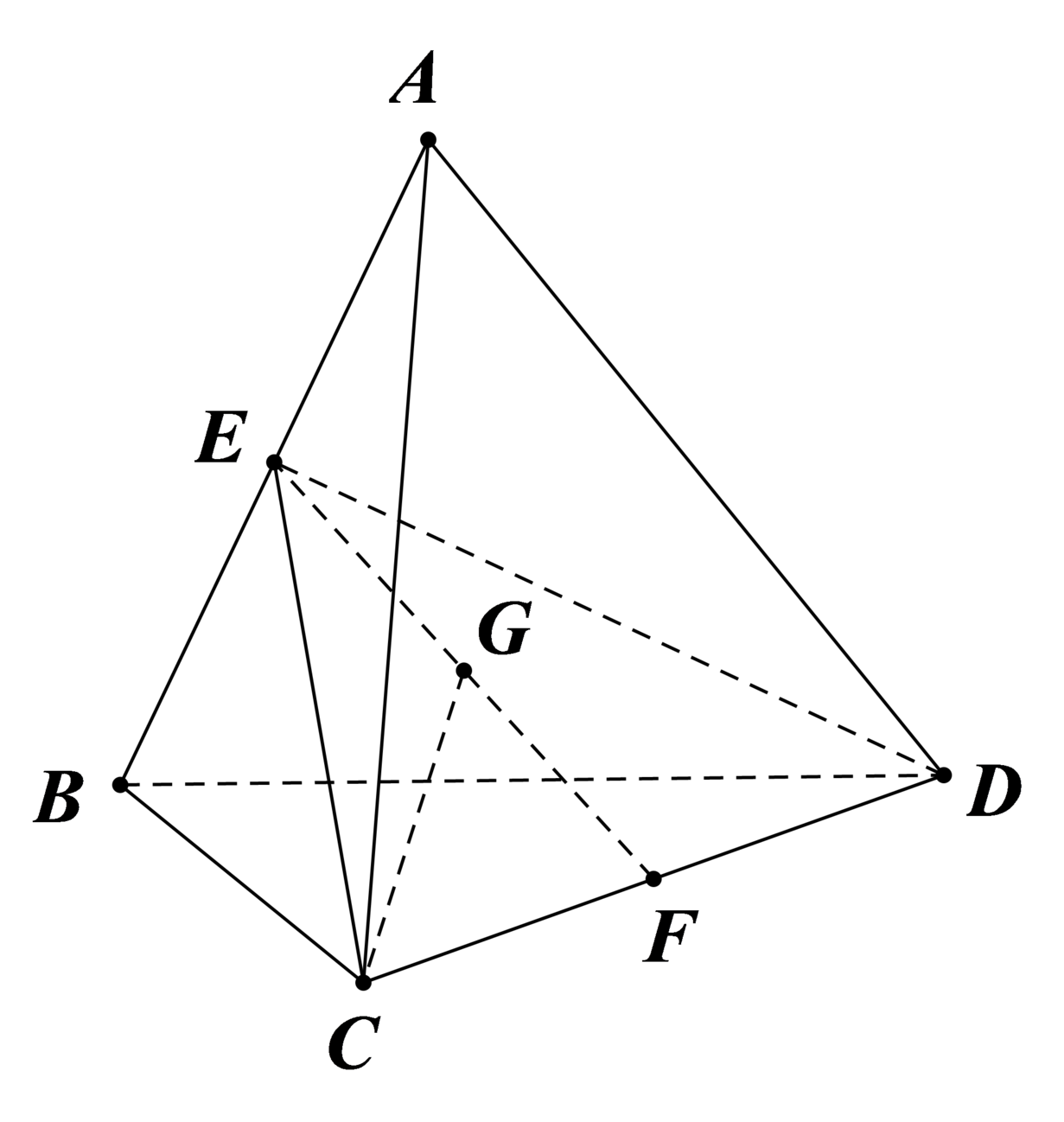
Gọi G là trung điểm của EF thì G chính là tâm mặt cầu ngoại tiếp tứ diện.
Ta có C E 2 = C B 2 + C A 2 2 − A B 2 4 = 6 2 + 6 2 2 − 2 2 4 = 35 ,
E F 2 = C E 2 − C F 2 = 35 − 2 2 = 31
⇒ G F = 31 2 ⇒ R = G C = G F 2 + C F 2 = 31 4 + 4 = 47 2 .
Vậy diện tích mặt cầu cần tính là:
S = 4 π R 2 = 4 π . 47 4 = 47 π .