Cho tam giác ABC vuông tại A biết AC = 21 cm và AB = 18 cm. Tìm khẳng định sai ?
A. C ^ = 41 °
B. B ^ = 49 °
C. B ^ = 50 °
D. B C = 3 85
Cho tam giác ABC vuông tại A, AB = 30 cm. Biết tan B = 8/15. Tìm khẳng định sai trong các khẳng định sau:
A. sin B = 7 17
B. cos B = 15 17
C. c o t B = 15 8
D. BC = 34
Câu 1:Cho tam giác A'B'C' đồng dạng vs tam giác ABC theo tỉ lệ đồng dạng k=1/2, diện tích tam giác A'B'C' là 20 cm vuông. TÍnh diện tích tam giác Abc
Câu 2: Cho tam giác ABC có AD là đường phân giác, biết AB=4,5 cm; AC= 7,2 cm;BD= 3,5 cm. Khi đó DC bằng bao nhiêu?
Câu 3: Cho tam giác ABC vuông tại A có AH là đường cao, BH=4 cm; HC= 9 cm. Khi đó AH bằng mấy?
Câu 4: Cho biết AB/CD=3/4 và CD = 12cm. Tính độ dài AB
Câu 5: Cho tam giác ABC lấy điểm M trên cạnh AB kẻ MN // BC(N thuộc AC) khẲNG= định nào sau đÂY LÀ SAI? kHẲNG ĐỊNH NÀO là đúng? giải thích ví sao lại đúng và vì sao lại sai
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai?
A. b = a.sinB = a.cosC
B. a = c.tanB = c.cotC
C. a 2 = b 2 + c 2
D. c = a.sinC = a.cosB
Đáp án B
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Ta có:
+ Theo định lý Pytago ta có a 2 = b 2 + c 2 nên C đúng
+ Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
b = asinB = acosC; c = asinC = acosB; b = ctanB = ccotC; c = btanC = bcotB
Nên A, D đúng
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai?
A. b = a.sin B = a.cos C
B. a = c.tan B = c.cot C
C. a 2 = b 2 + c 2
D. c = a.sin C = a.cos B
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Ta có:
+) Theo định lý Py-ta-go ta có a 2 = b 2 + c 2 nên C đúng.
+) Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
b = a.sin B = a.cos C; c = a.sin C = a.cos B; b = c.tan B = c.cot C;
C = b.tan C = b.cot B
Nên A, D đúng
Đáp án cần chọn là: B
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai?
A. b = a.sinB = a.cosC
B. a = c.tanB = c.cotC
C. a 2 = b 2 + c 2
D. c = a.sinC = a.cosB
Đáp án B
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Ta có:
+ Theo định lý Pytago ta có a 2 = b 2 + c 2 nên C đúng
+ Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
b = asinB = acosC; c = asinC = acosB; b = ctanB = ccotC; c = btanC = bcotB
Nên A, D đúng
Tam giác ABC có AB = 5 cm; BC = 6 cm và AC = 7 cm. Gọi A 1 ^ ; B 1 ^ ; C 1 ^ theo thứ tự là góc ngoài tại các đỉnh A, B, C của tam giác đó. Trong các khẳng định, khẳng định nào là đúng?
A. A 1 ^ > B 1 ^ > C 1 ^
B. B 1 ^ > C 1 ^ > A 1 ^
C. C 1 ^ > A 1 ^ > B 1 ^
D. C 1 ^ > B 1 ^ > A 1 ^
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH=24 cm và HC=18 cm. Tính: BH, ,BC,AC,AB và diện tích tam giác ABC Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB= 12 cm và BC=20 cm. Tính: BH, ,AC,HC,AH và diện tích tam giác ABC Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=3 cm và AC=4 cm. Tính: BH, ,BC,HC,AH và diện tích tam giác ABC Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC=15 cm và AH =12 cm. Tính: BH, ,BC,AB,AH và diện tích tam giác ABC Bài 5:Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=20 cm và HC=9cm. Tính: BH, ,BC,AC,AH và diện tích tam giác ABC
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Giải tam giác ABC vuông tại A biết
a. AB = 18 cm , BC = 21 cm
b.AB = 10 cm , AC = 6cm
a) Áp dụng Pytago ta có:
AB2 + AC2 = BC2
=> AC2 = BC2 - AB2 = 117
=> \(AC=\sqrt{117}\)
\(\sin C=\frac{AB}{BC}=\frac{18}{21}=\frac{6}{7}\)
=> \(\widehat{C}\approx59^0\)
=> \(\widehat{B}\approx31^0\)
b) Áp dụng Pytago ta có:
AB2 + AC2 = BC2
=> BC2 = 136
=> \(BC=\sqrt{136}\)
\(\tan C=\frac{AB}{AC}=\frac{10}{6}=\frac{5}{3}\)
=> \(\widehat{C}\approx59^0\)
=> \(\widehat{B}\approx31^0\)
Cho tam giác ABC có AB = 4,5 cm. Một đường thẳng d cắt đoạn AB, AC lần lượt tại M và N sao cho AM = 1,5cm, AN = 2 cm và NC = 5cm. Tìm khẳng định sai
A. MN// BC
B. MB = 3cm
C. Đường thẳng MN và BC có điểm chung.
Vì điểm M nằm giữa hai điểm A và B nên:
MB = AB – AM = 4,5 - 1,5 = 3cm
Ta có:
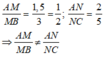
Do đó, đường thẳng MN không song song với BC.
Chọn đáp án A