Tìm giá trị nhỏ nhất của hàm số y = x 6 + 64 - x 6 bằng
A. 3 6 + 61 6
B. 1 + 65 6
C. 2
D. 2 32 6
Giá trị nhỏ nhất của hàm số y = 6 - x - x + 4 đạt tại x0, tìm x0?
A. x0 = -√10
B. x0 = -4
C. x0 = 6
D. x0 = √10
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a. y=\(\sqrt{\text{3(1+ sin(x))}}\)-5
b. y= 6 sin(x+8)-5
Tìm giá trị nhỏ nhất của hàm số y = x(x +2)(x+4)(x+6) + 18.
Cho hàm số y = 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x ∈ [−3; 4]
A. max − 3 ; 4 y = 4
B. min y = − 2 − 3 ; 4
C. Cả A, B đều đúng
D. Cả A, B đều sai
Hàm số y = 4 - x - x + 6 đạt giá trị nhỏ nhất tại x = x0. Tìm x0
A. x0 = -6
B. x0 = -1
C. x0 = 0
D. x0 = 4
Đáp án D
Điểu kiện

Xét -6 < x < 4, khi đó áp dụng công thức ![]() ta có:
ta có:

=> hàm số đã cho nghịch biến trên -6 < x ≤ 4
Vì vậy, hàm số đạt giá trị nhỏ nhất tại x0 = 4
Cho đồ thị: ( C ) : y = 3 x - 2 - 2 x - 6 Tìm giá trị lớn nhất và nhỏ nhất của hàm số với -3≤ x≤ 4
A. max y= 4; min y=2
B. max y= 2; min y= -4
C.max y=4; min y=-2
D. max y=2; min y= -2
Ta có: 
+Vẽ đường thẳng y= x với x≥3 đi qua hai điểm O(0; 0) và A(1;1) và lấy phần đường thẳng bên phải của đường thẳng x= 3.
+Vẽ đường thẳng y=5x-12 với 2≤ x≤ 3 đi qua hai điểm B(3;3) và C( 2; -2) và lấy phần đường thẳng nằm giữa của hai đường thẳng x=2; x=3.
+Vẽ đường thẳng y= -x đi qua hai điểm O và D( -1; -1) và lấy phần đường thẳng bên trái của đường thẳng x= 2
+ Dựa vào đồ thị hàm số ta có:
![]()
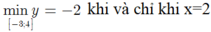
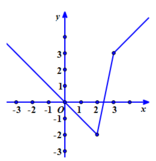
Chọn C.
tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
A. y =\(\sqrt{\text{6(1 + sin(x))}}-9\)
B.y = 4 sin(x+1)−7
Cho hai hàm số y=f(x),y=g(x) có đạo hàm là f'(x),g'(x) Đồ thị hàm số f'(x), g'(x) được cho như hinh vẽ dưới đây
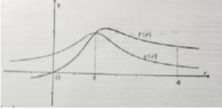
Biết rằng f(0)-f(6)<g(0)-g(6) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [0;6] lần lượt là:
A. h(6),h(2)
B. h(0),h(2)
C. h(2),h(6)
D. h(2),h(0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 1/sinx trên đoạn [ π /3; 5 π /6]
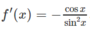
f′(x) < 0 nên và f’(x) > 0 trên ( π /2; 5 π /6] nên hàm số đạt cực tiểu tại x = π /2 và f CT = f( π /2) = 1
Mặt khác, f( π /3) = 2 3 , f(5 π /6) = 2
Vậy min f(x) = 1; max f(x) = 2
Cho hàm số y=f(x) có đạo hàm f’(x). Hàm số y=f’(x) liên tục trên tập số thực và có đồ thị như hình vẽ. Biết f - 1 = 13 4 , f 2 = 6 . Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số g x = f 3 x - 3 f x trên [-1;2] bằng
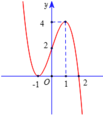
A. 1573 64
B. 198
C. 37
D. 42