Trong không gian Oxyz, cho vector a ⇀ = 2 i ⇀ -   j ⇀ - 2 k ⇀  Độ dài của véctơ a ⇀  bằng

Trong không gian với hệ tọa độ Oxyz, cho A(1;-1;2), B(0;1;1). Vector nào dưới đây cùng phương với A B ^  

A .   u → = ( 1 ; - 2 ; 1 )

B .   u → = ( 1 ; 2 ; - 1 )

C .   u → = ( 1 ; 2 ; 1 )

D .   u → = ( - 1 ; - 2 ; 1 )

Trong không gian Oxyz, cho  O M → = 3 i → - 2 j → +  k → . Tìm tọa độ của điểm M.

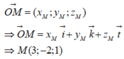
Trong không gian Oxyz, cho hai vector a → = a 1 , a 2 , a 3 , b → = b 1 , b 2 , b 3  khác 0 → . Tích có hướng của a →  và b →  là c → . Câu nào sau đây đúng?

A.   c → = a 2 b 3 - a 3 b 2 , a 3 b 1 - a 1 b 3 , a 1 b 2 - a 2 b 1

B.   c → = a 1 b 3 - a 2 b 1 , a 2 b 3 - a 3 b 2 , a 3 b 1 - a 1 b 3

C.   c → = a 1 b 3 - a 3 b 1 , a 2 b 2 - a 1 b 2 , a 3 b 2 - a 2 b 3

D.   c → = a 3 b 1 - a 1 b 3 , a 1 b 2 - a 2 b 1 , a 2 b 3 - a 3 b 1

Trong không gian Oxyz, cho vectơ O A → = j → - 2 k → . Tọa độ điểm A là

Trong không gian Oxyz, cho vectơ a → = 2 i → - j → - 2 k → . Độ dài của vectơ  a → bằng

A.  5

B. 9

C. 5

D. 3

Trong không gian Oxyz, cho O A → = i → + j → - 3 k → , B 2 ; 2 ; 1 . Tìm tọa độ điểm M thuộc trục tung sao cho M A 2 + M B 2 nhỏ nhất

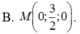
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P):2x-3y+z-2018=0 có vector pháp tuyến là:

A.  n → =(-2;3;-1) 

B.   n → =(2;3;1) 

C.  n → =(2;-3;1)

D.   n → =(2;-3;-1)

Trong không gian với hệ tọa độ Oxyz, mặt phẳng P :   2 x − 3 y + z − 2018 = 0  có vector pháp tuyến là:

A.  n → = − 2 ; 3 ; − 1

B.  n → = 2 ; 3 ; 1

C.  n → = 2 ; − 3 ; 1

D.  n → = 2 ; − 3 ; − 1