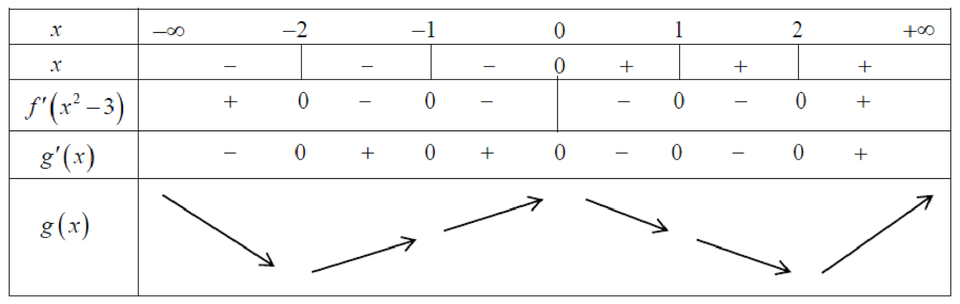
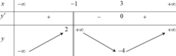
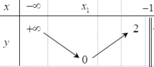
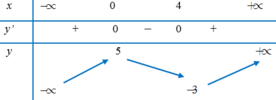
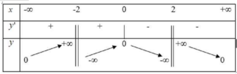
Cho hàm số y=f(x) xác định R ∖ {1}và liên tục trên và có bảng biến thiên như hình dưới đây
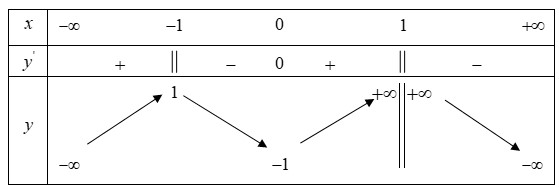
Hãy chọn khẳng định đúng
A. Hàm số có 3 cực trị
B. Hàm số đạt cực đại tại x=-1, cực tiểu tại x=0
C. Hàm số đạt cực đại tại x= ± 1, cực tiểu tại x=0
D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng -1

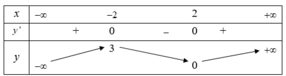



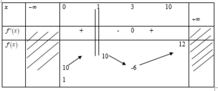
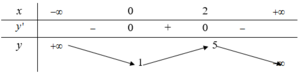


 .
.