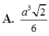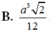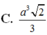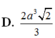Thể tích của khối tứ diện đều có tất cả các cạnh bằng 3 là:
A . 6 4
B . 3 6 4
C . 3 3
D . 3 2
Thể tích của khối tứ diện đều có tất cả các cạnh bằng 3 là:
A. 6 4
B. 3 6 4
C. 3 3
D. 3 2
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
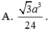
![]()
![]()
![]()
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
A. 3 a 3 24 .
B. 2 π a 3 24 .
C. 2 2 a 3 9 .
D. 3 π a 3 8 .
Đáp án B
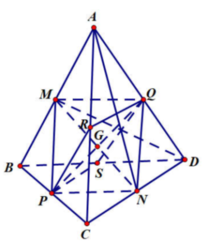
Gọi G là trọng tâm tứ diện ABCD. Ta chứng minh G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện.
Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, BC, AD, AC, BD.
Ta có G là trung điểm của các đoạn MN, PQ, RS.
Δ A C D = Δ B C D ⇒ A N = B N ⇒ Δ N A B cân tại N ⇒ M N ⊥ A B
Tương tụ ta có M N ⊥ C D .
Ta có: P Q = R S = M N = A N 2 − A M 2 = a 3 2 2 − a 2 4 = a 2 2 .
Suy ra d G , A B = d G , C D = 1 2 M N = a 2 4 .
Chứng minh tương tự ta có d G , A C = d G , A D = d G , B D = d G , B C = a 2 4
Vậy G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD.
Bán kính mặt cầu R = a 2 4 . Suy ra thể tích khối cầu là V = 4 3 π R 3 = 4 3 π a 2 4 3 = 2 π a 3 24 .
Tính thể tích của khối tứ diện đều có tất cả các cạnh bằng a.
A. 2 12 a 3
B. a 3
C. 6 a 3
D. 1 12 a 3
Tính thể tích của khối tứ diện đều có tất cả các cạnh bằng a.
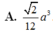
![]()
![]()
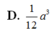
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Tính thể tích V của khối tứ diện ABCD
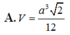
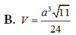
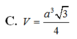
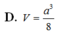
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Tính thể tích V của khối tứ diện ABCD
A. V = a 3 2 12
B. V = a 3 11 24
C. V = a 3 3 4
D. V = a 3 8
Cho khối tứ diện đều có tất cả các cạnh bằng 2a. Thể tích khối tứ diện đã cho bằng
A. a 3 2 6
B. a 3 2 12
C. a 3 2 3
D. 2 a 3 2 3
Cho khối tứ diện đều có tất cả các cạnh bằng 2a. Thể tích khối tứ diện đã cho bằng: