Bài tập số 4: Tìm số phức liên hợp \(\overline{Z}\) và tính modun (|z|) của số phức sau.

   a, z = 2 + 3i                                 b, \(z=\left(2+3i\right)^3\)

  c, \(z=\dfrac{2+3i}{1-2i}\)                                d, \(z=\sqrt{2}-\dfrac{4}{3}i\)

Tìm số phức liên hợp của số phức z=i(3i+1)

A. .

B. .

C. .

D.

Tìm số phức liên hợp của số phức  z = i ( 3 i + 1 )

A.  z ¯ = 3 + i

B.  z ¯ = − 3 + i

C.  z ¯ = 3 − i

D.  z ¯ = − 3 − i

Tìm số phức liên hợp của số phức z=i(3i+1)

A..

B..

C..

D.

Tìm số phức liên hợp của số phức z thỏa mãn (1+i)z = 1 + 3i

A.   z ¯ = -1 + 2i

B.   z ¯  = 1 - 2i

C.   z ¯  = -1 - 2i

D.   z ¯  = 1 + 2i

Tìm số phức liên hợp của số phức z=(2-3i)(1+i)

A.  z ¯ = 5 + i

B.  z ¯ = 5 - i

C.  z ¯ = - 5 + i

D.  z ¯ = - 5 - i

Cho số phức z, biết ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i .

Tìm số phức liên hợp của số phức w=3z-3i

A.  1 3 - 1 3 i

B.  1 3 + 1 3 i

C.  1 - 4 i

D.  1 + 4 i

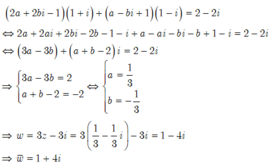
Cho số phức z thỏa mãn 2 i − 1 z = z ¯ 1 + i + 3 i . Tìm phần ảo của số phức liên hợp của z.

A. 2

B. -2

C. 2i

D. -2i

Cho số phức z thỏa mãn  2 i - 1 z   =   z ¯ 1 + i   +   3 i Tìm phần ảo của số phức liên hợp của z.

A. –2i

B. 2i

C. –2

D. 2